Question

A simple pendulum is set up in a trolley that moves to the right with acceleration $a$ on a horizontal plane. Then the thread of the pendulum in the mean position makes an angle $\theta$ with the vertical.
$\left(A\right)$ ${\tan }^{-1}\left({\displaystyle \frac{a}{g}}\right)$ In the forward direction
$\left(B\right)$ ${\tan }^{-1}\left({\displaystyle \frac{a}{g}}\right)$In the backward direction
$\left(C\right)$ ${\tan }^{-1}\left({\displaystyle \frac{g}{a}}\right)$ In the backward direction
$\left(D\right)$ ${\tan }^{-1}\left({\displaystyle \frac{g}{a}}\right)$ In the forward direction

Answer 1

Hint: For solving this type of problem we should be able to know the first simple pendulum function and how the change in motion changes the string tension and everything. Motion, length, amplitude, mass are things that affect the swing of the pendulum.

Complete step by step solution Here in this question it is given that a trolley has an acceleration$a$. As this trolley moves, their frame of reference also changes. Also, it is given that it makes some angle with the vertical. Therefore now through all this information, we will now be able to solve this problem.

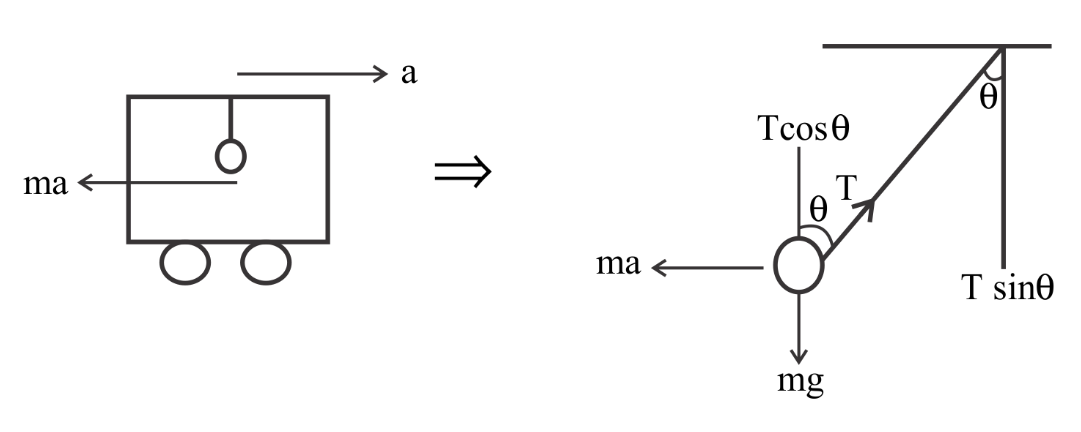
Now we will go in the frame of the trolley, so for this, we will have the following conditions
Also, there will be a pseudo force having $ma$ force in the opposite direction. This force will act when there is the ma force that is acting on the bob of the pendulum.
After a certain time the pendulum will make $\theta$ an angle from the mean position. So the new angle made by it will be as follows.
Tension on the string will be $T$ and the angles will be $T\cos \theta$ and $T\sin \theta$ as shown in the figure.
Due to gravity, there will be $mg$
Now balancing all four forces, we get
$$\Rightarrow mg=T\cos \theta$$
And the other equation will be
$\Rightarrow ma=T\sin \theta$
Now on dividing both the above equations, we get
$\Rightarrow {\displaystyle \frac{a}{g}}=\tan \theta$
Hence $\theta ={\tan }^{-1}\left({\displaystyle \frac{a}{g}}\right)$

So the answer will be $\theta ={\tan }^{-1}\left({\displaystyle \frac{a}{g}}\right)$in a backward direction.

Note: A setup could be a straightforward device composed of a weight suspended on a string, wire, metal, or different material that swings back and forth. Pendulums are utilized in gramps clocks and also they prefer to keep time.