
A simple pendulum makes 10 oscillations in 20 seconds. What is the time period and frequency of its oscillation?
Answer
120k+ views
Hint: The approach to solve this question is using relation of frequency with time period that is $f = \dfrac{1}{T}$ where f is the frequency and T is the time period, and unitary method , so putting values in formula is easy let us know little about unitary method which will also help you in the further problems.
Let us understand this concept with a basic example, assume that you are going to buy 12 balls cost 20 rupees so, 6 balls cost how many rupees:
For 12 balls we have 20 rupees
$12 \to 20$
For single for we have:
$1 \to \dfrac{{20}}{{12}} = \dfrac{5}{3}$
So, for 6 balls we have,
$6 \to 6 \times $$\dfrac{5}{3}$$ = 10$ rupees
Based on the above two concepts we will solve our question in an easy way.
Complete solution step by step:
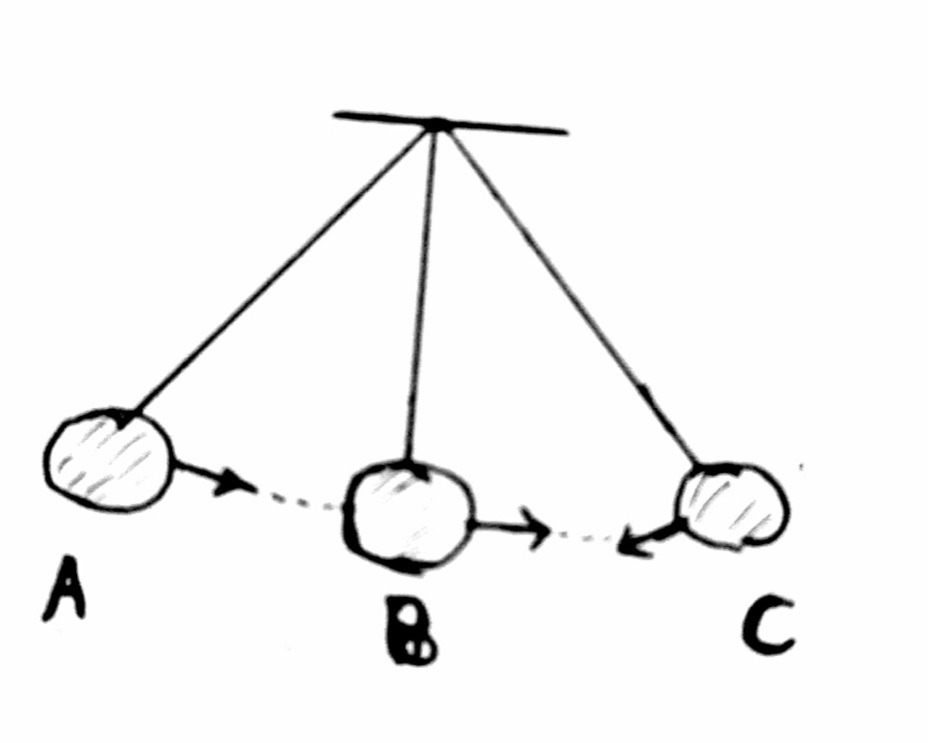
According to the question given let us discuss some of related terms with this question
Simple Pendulum is a very small heavy bob suspended at a point from a fixed support using a single thread so that it oscillates freely. The distance between the point of suspension and bob’s centre is
the length of pendulum
One oscillation: One complete to and fro motion of the oscillating body is called one oscillation.
Frequency: It is the number of oscillations made by the body in one second.
Time Period: It is the time taken by a body to complete one oscillation.
So, let's follow the calculations
As mentioned, 10 oscillations in 20 seconds
$
10 \to 20 \\
1 \to \dfrac{{10}}{{20}} = 0.5\sec \\
$
So, for a single oscillation time taken or what we say time period is 0.5 seconds.
Further calculating frequency
$
f = \dfrac{1}{T} \\
= \dfrac{1}{{0.5}} = 2hz \\
$
So, frequency is 2 hertz.
Note: The motion discussed above is considered in simple harmonic motion.
Let is discuss some important parts regarding this motion:
To study the motion of bob we use sine wave forms which comes from a derivation
The formula used for calculating displacement in simple harmonic motion is
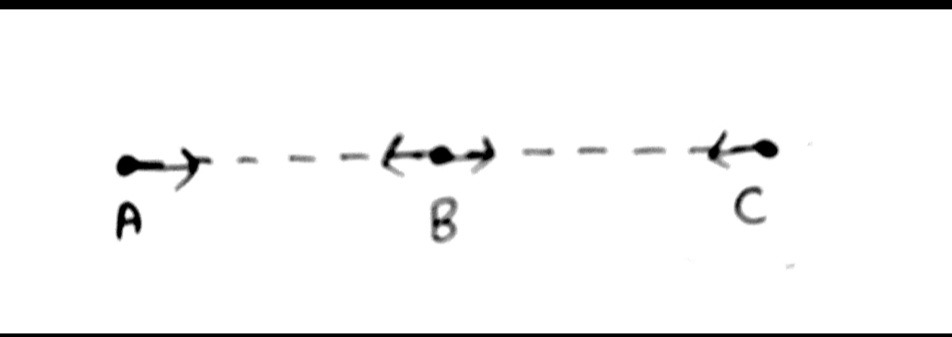
$s = A\sin \omega t$ where A is the amplitude or maximum displacement possible, w is the angular frequency and t is the time take to reach there so, by considering this formula our motion becomes like to and fro like in the diagram given where particle moves from B to C , then C to B , B to A , then back to B and this is called one complete cycle.
Let us understand this concept with a basic example, assume that you are going to buy 12 balls cost 20 rupees so, 6 balls cost how many rupees:
For 12 balls we have 20 rupees
$12 \to 20$
For single for we have:
$1 \to \dfrac{{20}}{{12}} = \dfrac{5}{3}$
So, for 6 balls we have,
$6 \to 6 \times $$\dfrac{5}{3}$$ = 10$ rupees
Based on the above two concepts we will solve our question in an easy way.
Complete solution step by step:

According to the question given let us discuss some of related terms with this question
Simple Pendulum is a very small heavy bob suspended at a point from a fixed support using a single thread so that it oscillates freely. The distance between the point of suspension and bob’s centre is
the length of pendulum
One oscillation: One complete to and fro motion of the oscillating body is called one oscillation.
Frequency: It is the number of oscillations made by the body in one second.
Time Period: It is the time taken by a body to complete one oscillation.
So, let's follow the calculations
As mentioned, 10 oscillations in 20 seconds
$
10 \to 20 \\
1 \to \dfrac{{10}}{{20}} = 0.5\sec \\
$
So, for a single oscillation time taken or what we say time period is 0.5 seconds.
Further calculating frequency
$
f = \dfrac{1}{T} \\
= \dfrac{1}{{0.5}} = 2hz \\
$
So, frequency is 2 hertz.
Note: The motion discussed above is considered in simple harmonic motion.
Let is discuss some important parts regarding this motion:
To study the motion of bob we use sine wave forms which comes from a derivation
The formula used for calculating displacement in simple harmonic motion is
$s = A\sin \omega t$ where A is the amplitude or maximum displacement possible, w is the angular frequency and t is the time take to reach there so, by considering this formula our motion becomes like to and fro like in the diagram given where particle moves from B to C , then C to B , B to A , then back to B and this is called one complete cycle.

Recently Updated Pages
Difference Between Circuit Switching and Packet Switching

Difference Between Mass and Weight

JEE Main Participating Colleges 2024 - A Complete List of Top Colleges

Sign up for JEE Main 2025 Live Classes - Vedantu

JEE Main 2025 Exam Pattern: Marking Scheme, Syllabus

JEE Main Course 2025 - Important Updates and Details

Trending doubts
JEE Main Chemistry Exam Pattern 2025

Charging and Discharging of Capacitor

Clemmenson and Wolff Kishner Reductions for JEE

JEE Main 2022 June 25 Shift 2 Question Paper with Answer Keys & Solutions

JEE Main Maths Paper Pattern 2025

JEE Main 2025 Helpline Numbers for Aspiring Candidates

Other Pages
NCERT Solutions for Class 11 Physics Chapter 7 Gravitation

Thermodynamics Class 11 Notes CBSE Physics Chapter 11 (Free PDF Download)

Mechanical Properties of Fluids Class 11 Notes CBSE Physics Chapter 9 (Free PDF Download)

NCERT Solutions for Class 11 Physics Chapter 3 Motion In A Plane

JEE Main 2022 June 27 Shift 2 Question Paper with Answer Keys & Solutions

NCERT Solutions for Class 11 Physics Chapter 4 Laws of Motion




