Question

A solid cube with an edge of 10cm is melted to form two equal cubes. Then ratio of the edge of the smaller cube to the edge of the bigger cube is
(a) ${{\left( \dfrac{1}{3} \right)}^{\dfrac{1}{3}}}$
(b) $\dfrac{1}{2}$
(c) ${{\left( \dfrac{1}{2} \right)}^{\dfrac{1}{3}}}$
(d) ${{\left( \dfrac{1}{4} \right)}^{\dfrac{1}{3}}}$

Answer 1

Hint: In this problem, we are given the dimensions of a solid cube. This cube has been melted to form two cubes having the same dimensions. We have to find the ratio of the edge of the smaller cube to the edge of the bigger cube. Edge of the smaller cube is given as 10cm. To find the edge of a smaller cube, we will let the edge of the cube be ‘a’.

Complete step-by-step solution:
Let’s solve the question now.

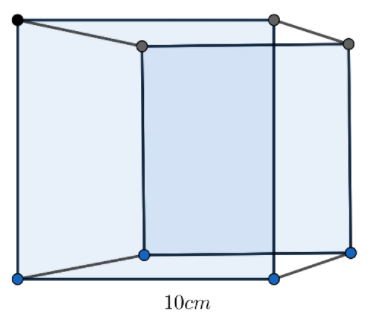
It is given that edge ‘l’ of the bigger cube = 10cm
So the volume of the bigger cube = ${{l}^{3}}\Leftrightarrow {{10}^{3}}=1000c{{m}^{3}}$

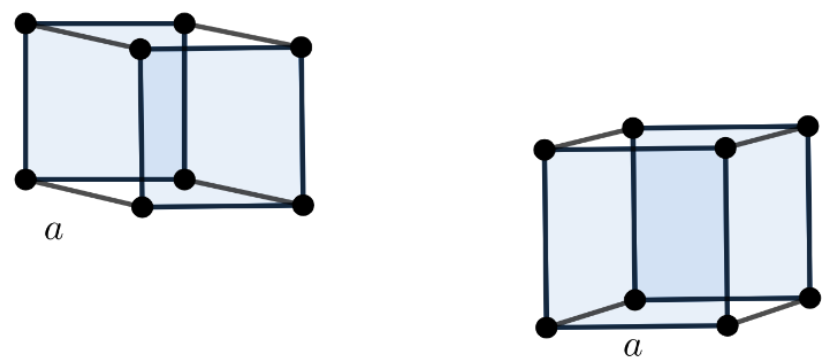
The cube is melted to form two smaller cubes of equal edges. So let the edge of the smaller cube be ‘a’. The volume of the two smaller cubes will be equal to the volume of the bigger cube.
$\begin{align}
  & \Rightarrow 1000c{{m}^{3}}={{a}^{3}}+{{a}^{3}} \\
 & \Rightarrow 1000c{{m}^{3}}=2{{a}^{3}} \\
\end{align}$
We need to find the value of ‘a’. Take 2 to the other side:
$\begin{align}
  & \Rightarrow \dfrac{1000c{{m}^{3}}}{2}={{a}^{3}} \\
 & \Rightarrow 500={{a}^{3}} \\
 & \Rightarrow \sqrt[3]{500}=a \\
\end{align}$
To find the cube root of 500, let’s take the LCM:
$\begin{align}
  & 2\left| \!{\underline {\,
  500 \,}} \right. \\
 & 2\left| \!{\underline {\,
  250 \,}} \right. \\
 & 5\left| \!{\underline {\,
  125 \,}} \right. \\
 & 5\left| \!{\underline {\,
  25 \,}} \right. \\
 & 5\left| \!{\underline {\,
  5 \,}} \right. \\
 & 1\left| \!{\underline {\,
  1 \,}} \right. \\
\end{align}$
LCM of 500: $2\times 2\times 5\times 5\times 5=5\sqrt[3]{4}$
We get the edge of smaller cube a = $5\sqrt[3]{4}$cm
Now, the ratio of the edge of the smaller cube to the edge of the bigger cube is:
$\Rightarrow \dfrac{5\sqrt[3]{4}}{10}=\dfrac{{{\left( 4 \right)}^{\dfrac{1}{3}}}}{2}$
As we know that $2\times 2\times 2=8$, so:
$\Rightarrow \dfrac{{{\left( 4 \right)}^{\dfrac{1}{3}}}}{2}={{\left( \dfrac{4}{8} \right)}^{\dfrac{1}{3}}}$
Now, cancel the terms we get:
$\Rightarrow {{\left( \dfrac{4}{8} \right)}^{\dfrac{1}{3}}}={{\left( \dfrac{1}{2} \right)}^{\dfrac{1}{3}}}$
So the correct answer is option (c).

Note: You should know the cube and cube roots of the numbers. Cube roots are formed by making triplets and square roots are formed by making pairs. SI units are most important to mention after the values. If they get missed, you will not be getting any marks.