
A solid cylinder rolls without slipping down a ${30^ \circ }$ slope. The minimum coefficient of friction needed to prevent slipping, will be:
A) $0.192$
B) $0.18$
C) $0.15$
D) $0.2$
Answer
220.2k+ views
Hint: The cylinder is rolling on a slope, as the given problem the cylinder is rolling, torque will be acting on the cylinder. This torque has a tendency to roll the cylinder and friction being an opposing force will oppose this rolling motion. The torque due friction must be balanced with the torque due to the weight of the cylinder. As no external force is acting on the cylinder, all the force acting on the cylinder must be balanced.
Complete step by step solution:
We are given that a cylinder is rolling on an inclined plane having slope of ${30^ \circ }$ . The surface of the inclined slope has friction. Friction by its nature is an opposing force, it will act in the opposite direction to the motion of the cylinder. Let us first draw the free body diagram of the system and label the forces acting on the solid cylinder.
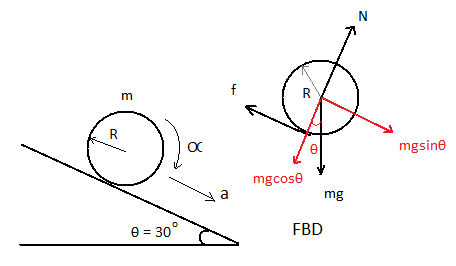
From the diagram, let the mass of the cylinder be $m$ and the radius be $R$ . $\theta $ is the angle of inclination of the slope which is given as $\theta = 3{0^ \circ }$ .
The force due to acceleration due to gravity is $mg$ , we have taken components of this force along the incline and in the direction opposite to the normal force.
$N$ is the normal force acting on the cylinder due to the surface of the inclined. $f$ is the frictional force acting on the cylinder. $\alpha $ is the angular acceleration of the cylinder.
From the diagram we have weight of block along normal to the plane is:
$W = N = mg\cos {30^ \circ }$-----equation $1$
The cylinder will roll in the downward direction, let the linear acceleration along the inclined be $a$ . The forces along the inclined will be:
$mgsin{30^ \circ } - f = ma$------equation $2$
Now, as the block will perform rolling motion, torque is responsible for this rolling motion. This torque will be given as:
$\tau = fR = I\alpha $
Here, $I$ is the moment of inertia of the cylinder. The moment of inertia of the cylinder along its axis of rotation is $I = \dfrac{{m{R^2}}}{2}$
Substituting this value in the above equation, we get:
$fR = \dfrac{{m{R^2}}}{2}\alpha $
$ \Rightarrow f = \dfrac{{mR}}{2}\alpha $
The relation between angular acceleration and linear acceleration $a$ is $a = R\alpha $ .
$ \Rightarrow f = \dfrac{{mR}}{2}\dfrac{a}{R}$
$ \Rightarrow f = \dfrac{{ma}}{2}$-------equation $3$
$ \Rightarrow a = \dfrac{{2f}}{m}$
Substituting this value in equation $2$ , we get
$mgsin{30^ \circ } - f = ma$
$ \Rightarrow mgsin{30^ \circ } - \dfrac{{ma}}{2} = ma$
$ \Rightarrow mg\left( {\dfrac{1}{2}} \right) = \dfrac{{3ma}}{2}$
$ \Rightarrow a = \dfrac{g}{3}$
Substituting this value in equation $3$ , we get
$f = \dfrac{{ma}}{2}$
$f = \dfrac{{ma}}{2} = \dfrac{m}{2} \times \dfrac{g}{3}$
$ \Rightarrow f = \dfrac{{mg}}{6}$
Frictional force is given as $f = \mu N$ , $\mu $ is the coefficient of friction.
From the figure we have achieved that: $N = mg\cos {30^ \circ }$ , therefore, we can have:
$f = \mu N = \mu mg\cos {30^ \circ }$
$ \Rightarrow \dfrac{{mg}}{6} = \mu mg\dfrac{{\sqrt 3 }}{2}$ as $\cos {30^ \circ } = \dfrac{{\sqrt 3 }}{2}$
$ \Rightarrow \mu = \dfrac{2}{{6\sqrt 3 }}$
$ \Rightarrow \mu = 0.192$
Therefore, the minimum coefficient of friction needed to prevent slipping, will be $\mu = 0.192$.
Option A is the correct option.
Note: Frictional force is opposing in nature. The forces on the cylinder must be balanced along the inclined and along the normal to the plane. The moment of inertia of a solid cylinder along its axis of rotation is given as $I = \dfrac{{m{R^2}}}{2}$ . The relation between linear acceleration and angular acceleration is given as $a = R\alpha $ . The components of forces must be taken properly.
Complete step by step solution:
We are given that a cylinder is rolling on an inclined plane having slope of ${30^ \circ }$ . The surface of the inclined slope has friction. Friction by its nature is an opposing force, it will act in the opposite direction to the motion of the cylinder. Let us first draw the free body diagram of the system and label the forces acting on the solid cylinder.

From the diagram, let the mass of the cylinder be $m$ and the radius be $R$ . $\theta $ is the angle of inclination of the slope which is given as $\theta = 3{0^ \circ }$ .
The force due to acceleration due to gravity is $mg$ , we have taken components of this force along the incline and in the direction opposite to the normal force.
$N$ is the normal force acting on the cylinder due to the surface of the inclined. $f$ is the frictional force acting on the cylinder. $\alpha $ is the angular acceleration of the cylinder.
From the diagram we have weight of block along normal to the plane is:
$W = N = mg\cos {30^ \circ }$-----equation $1$
The cylinder will roll in the downward direction, let the linear acceleration along the inclined be $a$ . The forces along the inclined will be:
$mgsin{30^ \circ } - f = ma$------equation $2$
Now, as the block will perform rolling motion, torque is responsible for this rolling motion. This torque will be given as:
$\tau = fR = I\alpha $
Here, $I$ is the moment of inertia of the cylinder. The moment of inertia of the cylinder along its axis of rotation is $I = \dfrac{{m{R^2}}}{2}$
Substituting this value in the above equation, we get:
$fR = \dfrac{{m{R^2}}}{2}\alpha $
$ \Rightarrow f = \dfrac{{mR}}{2}\alpha $
The relation between angular acceleration and linear acceleration $a$ is $a = R\alpha $ .
$ \Rightarrow f = \dfrac{{mR}}{2}\dfrac{a}{R}$
$ \Rightarrow f = \dfrac{{ma}}{2}$-------equation $3$
$ \Rightarrow a = \dfrac{{2f}}{m}$
Substituting this value in equation $2$ , we get
$mgsin{30^ \circ } - f = ma$
$ \Rightarrow mgsin{30^ \circ } - \dfrac{{ma}}{2} = ma$
$ \Rightarrow mg\left( {\dfrac{1}{2}} \right) = \dfrac{{3ma}}{2}$
$ \Rightarrow a = \dfrac{g}{3}$
Substituting this value in equation $3$ , we get
$f = \dfrac{{ma}}{2}$
$f = \dfrac{{ma}}{2} = \dfrac{m}{2} \times \dfrac{g}{3}$
$ \Rightarrow f = \dfrac{{mg}}{6}$
Frictional force is given as $f = \mu N$ , $\mu $ is the coefficient of friction.
From the figure we have achieved that: $N = mg\cos {30^ \circ }$ , therefore, we can have:
$f = \mu N = \mu mg\cos {30^ \circ }$
$ \Rightarrow \dfrac{{mg}}{6} = \mu mg\dfrac{{\sqrt 3 }}{2}$ as $\cos {30^ \circ } = \dfrac{{\sqrt 3 }}{2}$
$ \Rightarrow \mu = \dfrac{2}{{6\sqrt 3 }}$
$ \Rightarrow \mu = 0.192$
Therefore, the minimum coefficient of friction needed to prevent slipping, will be $\mu = 0.192$.
Option A is the correct option.
Note: Frictional force is opposing in nature. The forces on the cylinder must be balanced along the inclined and along the normal to the plane. The moment of inertia of a solid cylinder along its axis of rotation is given as $I = \dfrac{{m{R^2}}}{2}$ . The relation between linear acceleration and angular acceleration is given as $a = R\alpha $ . The components of forces must be taken properly.
Recently Updated Pages
Mass vs Weight: Key Differences Explained for Students

Electricity and Magnetism Explained: Key Concepts & Applications

JEE Energetics Important Concepts and Tips for Exam Preparation

JEE Isolation, Preparation and Properties of Non-metals Important Concepts and Tips for Exam Preparation

JEE Main 2021 July 25 Shift 1 Question Paper with Answer Key

JEE Main 2021 July 22 Shift 2 Question Paper with Answer Key

Trending doubts
JEE Main 2026: Application Form Open, Exam Dates, Syllabus, Eligibility & Question Papers

Understanding Uniform Acceleration in Physics

Derivation of Equation of Trajectory Explained for Students

Hybridisation in Chemistry – Concept, Types & Applications

Understanding the Angle of Deviation in a Prism

How to Convert a Galvanometer into an Ammeter or Voltmeter

Other Pages
Thermodynamics Class 11 Physics Chapter 11 CBSE Notes - 2025-26

JEE Advanced Marks vs Ranks 2025: Understanding Category-wise Qualifying Marks and Previous Year Cut-offs

Units And Measurements Class 11 Physics Chapter 1 CBSE Notes - 2025-26

NCERT Solutions For Class 11 Physics Chapter 8 Mechanical Properties Of Solids

Motion in a Straight Line Class 11 Physics Chapter 2 CBSE Notes - 2025-26

Laws of Motion Class 11 Physics Chapter 4 CBSE Notes - 2025-26




