
A solid non-conducting sphere of radius

Answer
417.9k+ views
Hint: From the Gauss Law of Electrostatics we can find out the electric field.The electric field inside a non-conducting sphere is
Complete step by step answer:
From the Gauss Law of Electrostatics we know,
In the given figure O is the centre. Let
Charge enclosed by the sphere
The radius of the cavity is given as
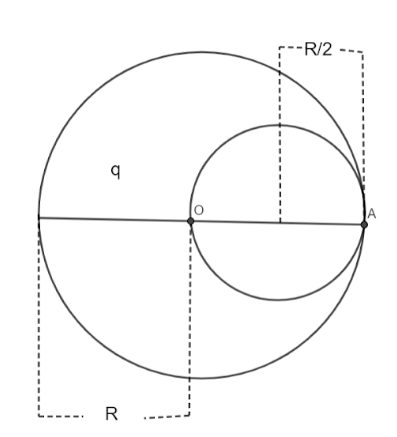
Let the volume charge density over radius
So, the charge
Substituting these values in equation
Thus now we get the electric field
Note: Gauss Law is applicable in many cases as it is shown here. The electric field inside both a hollow sphere and a non-conducting sphere is
Complete step by step answer:
From the Gauss Law of Electrostatics we know,
In the given figure O is the centre. Let
Charge enclosed by the sphere
The radius of the cavity is given as

Let the volume charge density over radius
So, the charge
Substituting these values in equation
Thus now we get the electric field
Note: Gauss Law is applicable in many cases as it is shown here. The electric field inside both a hollow sphere and a non-conducting sphere is
Recently Updated Pages
Master Class 9 General Knowledge: Engaging Questions & Answers for Success

Master Class 9 English: Engaging Questions & Answers for Success

Master Class 9 Science: Engaging Questions & Answers for Success

Master Class 9 Social Science: Engaging Questions & Answers for Success

Master Class 9 Maths: Engaging Questions & Answers for Success

Class 9 Question and Answer - Your Ultimate Solutions Guide

Trending doubts
Give 10 examples of unisexual and bisexual flowers

Draw a labelled sketch of the human eye class 12 physics CBSE

Differentiate between homogeneous and heterogeneous class 12 chemistry CBSE

Differentiate between insitu conservation and exsitu class 12 biology CBSE

What are the major means of transport Explain each class 12 social science CBSE

a Tabulate the differences in the characteristics of class 12 chemistry CBSE




