Question

A sphere is inscribed in the tetrahedron whose faces are $x=0,y=0,z=0$ and $2x+6y+3z-14=0$. Find its center and radius.
$\begin{align}
  & \text{A}\text{. }\left( \dfrac{7}{2},\dfrac{7}{2},\dfrac{7}{2} \right),\dfrac{7}{2} \\
 & \text{B}\text{. }\left( \dfrac{7}{9},\dfrac{7}{9},\dfrac{7}{9} \right),\dfrac{7}{9} \\
 & \text{C}\text{. }\left( \dfrac{7}{2},\dfrac{7}{2},\dfrac{7}{2} \right),\dfrac{7}{9} \\
 & \text{D}\text{. None of these} \\
\end{align}$

Answer 1

Hint: As given in the question the sphere is inscribed in the tetrahedron, so the length of the perpendicular from the center upon each of the faces of the tetrahedron is equal to the radius of the sphere. Then, by using the distance formula of a point from the plane is used to obtain the desired answer.
If $\left( l,m,n \right)$ is a point and $ax+by+cz=d$ is a plane, the distance formula will be
$\dfrac{d-ax-by-cz}{\sqrt{{{a}^{2}}+{{b}^{2}}+{{c}^{2}}}}$

Complete step-by-step solution:
If $\left( l,m,n \right)$ is a point and $ax+by+cz=d$ is a plane, the distance formula will be
$\dfrac{d-ax-by-cz}{\sqrt{{{a}^{2}}+{{b}^{2}}+{{c}^{2}}}}$
We have given that a sphere is inscribed in the tetrahedron whose faces are $x=0,y=0,z=0$ and $2x+6y+3z-14=0$.
We have to find its center and radius.
Let $\left( a,b,c \right)$ be the center and $r$ is the radius of the sphere inscribed in the tetrahedron.
As given the sphere is inscribed in the tetrahedron, so the length of the perpendicular from the center $\left( a,b,c \right)$ upon each of the faces of the tetrahedron is equal to the radius of the sphere. So, mathematically we represent it as
$\dfrac{a}{1}=\dfrac{b}{1}=\dfrac{c}{1}=r..............(i)$

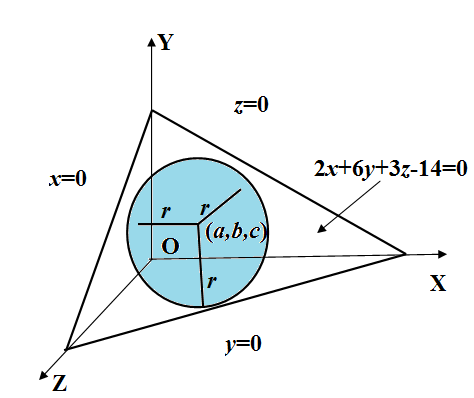
Now, we know that the distance formula is given as $\dfrac{d-ax-by-cz}{\sqrt{{{a}^{2}}+{{b}^{2}}+{{c}^{2}}}}$
Where, $\left( l,m,n \right)$ is a point and $ax+by+cz=d$ is a plane
Now, we have points $\left( a,b,c \right)$ and plane given in the question is $2x+6y+3z-14=0$
When we substitute the values in the distance formula, we get
\[\begin{align}
  & \Rightarrow \dfrac{14-2a-6b-3c}{\sqrt{{{2}^{2}}+{{6}^{2}}+{{3}^{2}}}} \\
 & \Rightarrow \dfrac{14-2a-6b-3c}{\sqrt{4+36+9}} \\
 & \Rightarrow \dfrac{14-2a-6b-3c}{\sqrt{49}} \\
 & \Rightarrow \dfrac{14-2a-6b-3c}{7}.....................(ii) \\
\end{align}\]
Now, equating equation (i) and (ii), we get
\[a=b=c=r=\dfrac{14-2a-6b-3c}{7}\]
\[a=b=c=r=\dfrac{14-2a-6b-3c}{7}\]
As $a=b=c$ , so the above equation becomes
\[\begin{align}
  & a=\dfrac{14-2a-6a-3a}{7} \\
 & 7a=14-11a \\
 &\Rightarrow 7a+11a=14 \\
 &\Rightarrow 18a=14 \\
 &\Rightarrow a=\dfrac{14}{18} \\
 &\Rightarrow a=\dfrac{7}{9} \\
\end{align}\]
As $a=b=c$, so \[a=\dfrac{7}{9};b=\dfrac{7}{9};c=\dfrac{7}{9};r=\dfrac{7}{9}\]
We get center of the sphere $\left( \dfrac{7}{9},\dfrac{7}{9},\dfrac{7}{9} \right)$ and radius $\dfrac{7}{9}$.
So the option B is the correct answer.

Note: We note the equations of the given planes $x=0,y=0,z=0$ correspond to coordinate planes $yz-$plane, $zx-$plane and $xy-$plane respectively in space. So $\left( a,b,c \right)$ represent direction ratios of the line passing through origin and $\left( a,b,c \right)$ and hence $\dfrac{a}{1},\dfrac{b}{1},\dfrac{c}{1}$ becomes the distance from $yz-$plane, $zx-$plane and $xy-$plane respectively. The sphere inscribed in a polyhedron is called insphere. We can alternatively solve using the equation touching the coordinate planes ${{x}^{2}}+{{y}^{2}}+{{z}^{2}}-2\lambda \left( x+y+z \right)+2{{\lambda }^{2}}=0$ where center is $\left( \lambda ,\lambda ,\lambda \right)$ and radius $\lambda $.