Question

A sphere of mass M and radius R is moving on a rough fixed surface, having coefficient of friction$\left( \mu \right)$ as shown in the figure below. It will attain a minimum linear velocity after time: \[({{v}_{0}}>\omega R)\]

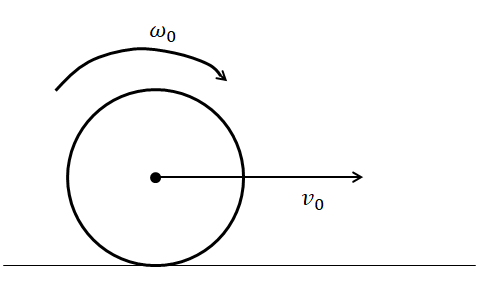
$A.\quad \dfrac{{{v}_{0}}}{\mu g}$
$B.\quad \dfrac{{{\omega }_{0}}R}{\mu g}$
$C.\quad \dfrac{2({{v}_{0}}-{{\omega }_{0}}R)}{5\mu g}$
$D.\quad \dfrac{2({{v}_{0}}-{{\omega }_{0}}R)}{7\mu g}$

Answer 1

Hint: Here, we first need to find the velocity of the sphere at the point (P) will be the sum of the velocity at P with respect to the center of mass and the velocity of the sphere’s center of mass. Hence; $\overline{{{v}_{p}}}=\overline{{{v}_{p-cm}}}+\overline{{{v}_{cm}}}$. The frictional force acting on the body is; ${{f}_{\mu }}=-\mu N=-\mu Mg$. Equating the frictional force with F=Ma, we will find the acceleration (a). Then using the law of motion:$v=u+at$, we will find the velocity at time (t), which is (${v}'$). The torque acting on the sphere will be, \[\left| \tau \right|=\left| {{f}_{\mu }}R \right|=\left| I\alpha \right|\]. After finding the value of angular acceleration \[(\alpha )\], we will find the angular frequency (${\omega }'$) at a later time (t) using: $\omega ={{\omega }_{0}}+\alpha t$. Finally using the condition to attain the minimum linear velocity, the frictional force must be zero, that is: \[{v}'={\omega }'R\], we can find the value of the time after which minimum linear velocity will be attained.

Step by step solution:
Let’s consider all the information given in the problem.

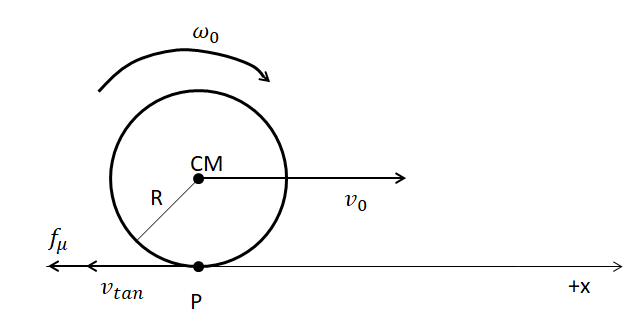
Let the point (P) be the point of contact between the sphere and the surface. Then the velocity of the sphere at the point (P) will be the sum of the velocity at P with respect to the center of mass and the velocity of the sphere’s center of mass. Hence; $\overline{{{v}_{p}}}=\overline{{{v}_{p-cm}}}+\overline{{{v}_{cm}}}$. The value of the velocity at P with respect to the center of mass, is the tangential velocity of the sphere, that is; $\overline{{{v}_{p-cm}}}={{\omega }_{o}}R.$However, the direction of this velocity component is against the direction of motion of the body. Therefore; $\overline{{{v}_{p}}}=\overline{{{v}_{p-cm}}}+\overline{{{v}_{cm}}}\Rightarrow \overline{{{v}_{p}}}=\left[ -{{\omega }_{0}}R+{{v}_{0}} \right]\Rightarrow \overline{{{v}_{p}}}=\left( {{v}_{0}}-{{\omega }_{0}}R \right)$. Since, we have the condition given in the problem that \[({{v}_{0}}>\omega R)\].
Further, the frictional force acting on the body is against the direction of motion. Hence, the frictional force is; ${{f}_{\mu }}=-\mu N=-\mu Mg$.
To attain the minimum linear velocity, the frictional force must be zero. Hence, the action of the body becomes rolling. Therefore, the new relation after time t for the minimum velocity$({v}')$is: \[{v}'={\omega }'R\], where$\left( {{\omega }'} \right)$ is the new angular frequency after time (t).
We will equate the frictional force with the force equation (F=Ma) to find the acceleration value of the sphere.
That is: $-\mu Mg=Ma\Rightarrow a=-\mu g$.
Then we will find the final velocity using the law of motion:$v=u+at$. Therefore; ${v}'={{v}_{0}}+at\Rightarrow {v}'={{v}_{0}}-\mu gt\to (1)$.
Now, let’s find the magnitude of torque acting on the sphere due to the frictional force is; \[\left| \tau \right|=\left| {{f}_{\mu }}R \right|=\left| I\alpha \right|\]. Here, $\alpha $ is the angular acceleration of the body and I is the moment of inertia of the sphere. We know that the moment of inertia of a sphere is;$I=\dfrac{2}{5}M{{R}^{2}}$.
Hence, the above equation becomes; \[\left| \tau \right|=\left| {{f}_{\mu }}R \right|=\left| I\alpha \right|\Rightarrow \mu NR=\dfrac{2}{5}M{{R}^{2}}\alpha \Rightarrow \alpha =\dfrac{5\mu MgR}{2M{{R}^{2}}}=\dfrac{5\mu g}{2R}\]. Therefore; $\alpha =\dfrac{5\mu g}{2R}$.
Now, we will use the circular motion formula to find the angular frequency at later time. That is; $\omega ={{\omega }_{0}}+\alpha t\Rightarrow {\omega }'={{\omega }_{0}}+\dfrac{5\mu g}{2R}t\Rightarrow {\omega }'R={{\omega }_{0}}R+\dfrac{5\mu gt}{2}\to (2)$
For the time (t) at which the frictional force acting on the sphere becomes zero, the equations (1) and (2) become equal due to the relation: \[{v}'={\omega }'R\]. Hence, ${{v}_{0}}-\mu gt={{\omega }_{0}}R+\dfrac{5\mu gt}{2}\Rightarrow {{v}_{0}}-{{\omega }_{0}}R=\dfrac{5\mu gt}{2}+\mu gt\Rightarrow {{v}_{0}}-{{\omega }_{0}}R=\dfrac{7\mu gt}{2}$.
Therefore, the value of time to attain minimum linear velocity is; ${{v}_{0}}-{{\omega }_{0}}R=\dfrac{7\mu gt}{2}\Rightarrow 2\left( {{v}_{0}}-{{\omega }_{0}}R \right)=7\mu gt\Rightarrow t=\dfrac{2\left( {{v}_{0}}-{{\omega }_{0}}R \right)}{7\mu g}$, given by Option D.

Note: Remember the relation between the linear motion variables and the circular motion variables, such as $v=\omega R$, where v is the tangential velocity and $\omega $ is the angular frequency and r is the radius of the circular motion. The angular displacement $\theta $ is; $\theta =\dfrac{s}{r}$, where s is the linear displacement. Similarly, the angular acceleration $\alpha $ is; $\alpha =\dfrac{a}{r}$, where a is the linear acceleration.