Question

A spherical glass vessel has a cylindrical neck 8 cm long, 2 cm in diameter; the diameter of the spherical part is 8.5 cm. By measuring the amount of water it holds, a child finds its volume to be \[345\text{ c}{{\text{m}}^{3}}\]. Check whether she is correct, taking the above as the inside measurements and \[\pi =3.14\].

Answer 1

Hint: Draw the diagram of the vessel to get a clear idea about the question. Now the total volume of the vessel would constitute the volume of cylindrical neck and volume of the spherical part. Use the volume of cylinder \[=\pi {{r}^{2}}h\] and volume of the sphere \[=\dfrac{4}{3}\pi {{r}^{3}}\] to find the required volume.

Complete step-by-step answer:
We are given a spherical glass vessel that has a cylindrical neck 8 cm long and 2 cm in diameter. The diameter of the spherical part is 8.5 cm. We have to find its volume and compare it with the child’s volume who found it to be \[345\text{ c}{{\text{m}}^{3}}\].
Let us diagrammatically consider this vessel,

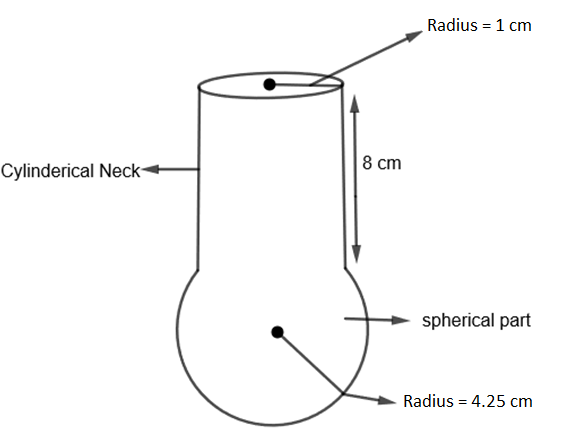
Here, we have to find the volume of the above vessel. We know that volume of vessel = Volume of cylindrical neck + Volume of the spherical part.
Let us consider the volume of the cylindrical neck as \[{{V}_{C}}\].
Also, let us consider the volume of the spherical part as \[{{V}_{S}}\].
Therefore, we get, the volume of the vessel (V) =\[{{V}_{C}}+{{V}_{S}}....\left( i \right)\]
Now, we know that volume of the cylinder \[=\pi {{r}^{2}}h\] where r is the radius of the cylinder, and h is the height of the cylinder.
We are given that the diameter of the cylindrical neck = 2 cm.
We know that, \[\text{radius =}\dfrac{\text{Diameter}}{2}=\dfrac{2}{2}=1\text{ cm}\]
Also, we are given the height of the cylindrical neck = 8 cm.
By substituting the value of radius and height in the volume of the cylinder, we get,
The volume of the cylindrical neck \[\left( {{V}_{C}} \right)=\pi {{\left( 1 \right)}^{2}}.8\text{ c}{{\text{m}}^{3}}\]
\[\Rightarrow {{V}_{C}}=8\pi \text{ c}{{\text{m}}^{3}}\]
Now, we know that volume of the sphere \[=\dfrac{4}{3}\pi {{r}^{3}}\]
We are given that diameter of the spherical part = 8.5 cm.
We know that \[\text{radius =}\dfrac{\text{Diameter}}{2}=\dfrac{8.5}{2}=4.25\text{ cm}\]
By substituting the value of radius in the volume of the sphere, we get,
The volume of the spherical part \[{{V}_{S}}=\dfrac{4}{3}\pi {{\left( 4.25 \right)}^{3}}\text{c}{{\text{m}}^{3}}\]
\[\Rightarrow {{V}_{S}}=102.35\pi \text{ c}{{\text{m}}^{3}}\]
By substituting the values of \[{{V}_{C}}\] and \[{{V}_{S}}\] in equation (i), we get
The volume of the Vessel, \[(V)=8\pi \text{ }c{{m}^{3}}+102.35\pi \text{ }c{{m}^{3}}\]
By taking \[\pi \] common, we get,
\[V=\pi \left( 8+102.35 \right)\text{c}{{\text{m}}^{3}}\]
We are given that, \[\pi =3.14\]. So, we get,
\[V=\left( 3.14 \right)\times \left( 110.35 \right)\text{c}{{\text{m}}^{3}}\]
\[=346.499\text{ c}{{\text{m}}^{3}}\]
Therefore, we get the volume of the vessel equal to \[346.499\text{ c}{{\text{m}}^{3}}\]. Hence, the child is incorrect because she found the volume equal to \[345\text{ c}{{\text{m}}^{3}}\] while actual volume is \[346.499\text{ c}{{\text{m}}^{3}}\].

Note: Students often forget to convert diameter into radius and substitute the value of diameter in place of the radius. So this must be taken care of. Also, students must note that the total volume of any object always constitutes each of its parts so that total volume could be taken into account.