Question

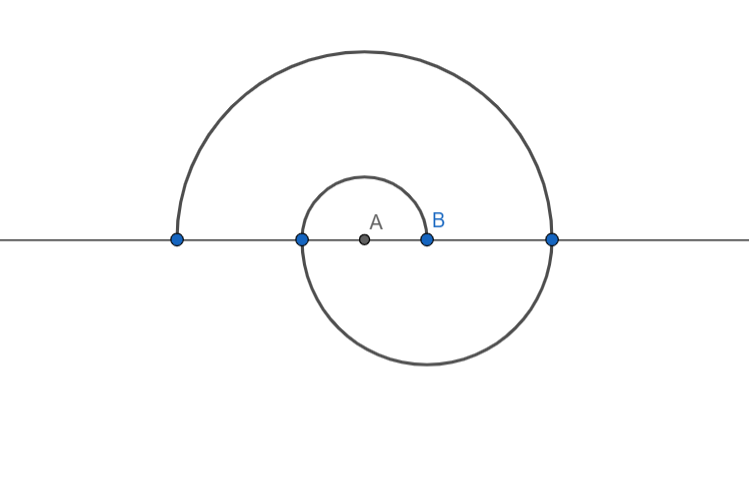
A spiral is made of successive semicircles with centres alternatively at A and B, starting with A, of radii 0.5cm, 1cm, 1.5cm, 2cm, … as shown in the figure below. What is the total length of the spiral consisting of 13 such spirals. Use $\pi =\dfrac{22}{7}$

Answer 1

Hint: Observe that the radii here are in A.P. Since circumference of cirlce $\propto r$,the lengths of semicircles will also be in A.P. Find the common difference and first term of that A.P. Use ${{S}_{n}}=\dfrac{n}{2}\left( 2a+\left( n-1 \right)d \right)$ for finding total length of the spiral.

Complete step-by-step answer:

We know that if $\left\{ {{a}_{n}} \right\}$ is an A.P with common difference d then $\left\{ k{{a}_{n}} \right\}$ is also an A.P with common difference kd.
Here Sequence of radii is 0.5cm, 1cm, 1.5cm, 2cm, … which is clearly an A.P with first term a = 0.5cm and common difference 1-0.5 =0.5cm.
Also Length of semicircle $=\pi r$
So the sequence of lengths of semicircles will also be an A.P with common difference $=0.5\pi cm$ and the first term will be $0.5\pi cm$.
Now we know that ${{S}_{n}}=\dfrac{n}{2}\left( 2a+\left( n-1 \right)d \right)$
Put n = 13, $a=0.5\pi cm$ and $d=0.5\pi cm$, we get
$\begin{align}
  & {{S}_{13}}=\dfrac{13}{2}\left( 2\times 0.5\pi +\left( 13-1 \right)0.5\pi \right)cm \\
 & =\dfrac{13}{2}\left( \pi +6\pi \right)cm \\
 & =\dfrac{91}{2}\pi cm \\
\end{align}$
Substituting $\pi =\dfrac{22}{7}$, we get
\[{{S}_{13}}=\dfrac{91}{2}\times \dfrac{22}{7}=143cm\]
Since ${{S}_{n}}$ is the sum of lengths of first n spirals ${{S}_{13}}$ will be the total length of the spiral consisting of 13 consecutive semicircles.
Hence the total length of the spiral consisting of 13 such spirals is 143cm.

Note: [1] If $\left\{ {{a}_{n}} \right\}$ is an A.P with common difference d then $\left\{ k{{a}_{n}} \right\}$ is also an A.P with common difference kd. This statement can be proved with simple calculations:
$\left\{ {{a}_{n}} \right\}=\left\{ a,a+d,a+2d,...,a+\left( n-1 \right)d \right\}$
so $\left\{ k{{a}_{n}} \right\}=\left\{ ka,ka+kd,ka+2kd,...,ka+\left( n-1 \right)kd \right\}$
Hence the first term of the sequence $\left\{ k{{a}_{n}} \right\}$ is ka and the common difference is kd.
[2] If $\left\{ {{a}_{n}} \right\},\left\{ {{b}_{n}} \right\}$ are two A.Ps, then so is $\left\{ {{a}_{n}}+{{b}_{n}} \right\},\left\{ {{a}_{n}}+k \right\}$ and $\left\{ k{{a}_{n}} \right\}$