Question

A square has one vertex on the parabola ${y^2} = 4ax$ and the diagonal through this vertex lies along the axis of the parabola. If the ends of the other diagonal lie on the parabola, the coordinates of one of the vertices of the square is
A) \[\left( {0,2a} \right)\]
B) \[\left( {4a,4a} \right)\]
C) \[\left( {a, - 2a} \right)\]
D) None of these

Answer 1

Hint:
We can draw a parabola opened to the right. We can draw a square with vertices on the origin, on the either sides of the parabola and on the x axis and mark the square. Then we can find the coordinates in the parametric form. Then we can calculate the slope using the points and equate it to the slope of the same line by taking the tangent of the angle that it makes the x axis. We can equate this as a solution for t. on substituting back, we get the required coordinates.

Complete step by step solution:
We can draw the given parabola which is open to the right. We can draw a square ABCD with one vertex A in the vertex of the parabola which is the origin and the adjacent vertices B and D on the parabola. Then C will be a point on the X axis.

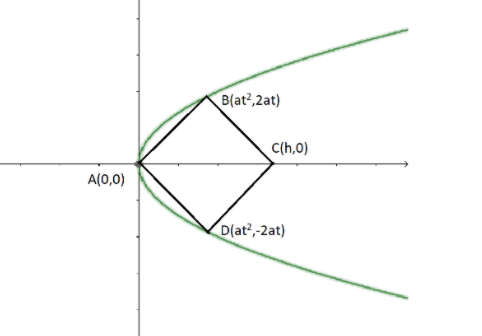
We know that the parametric form of a point on a parabola is given by $\left( {a{t^2},2at} \right)$ .
As the parabola is symmetric to the x axis, we can take the point B as $\left( {a{t^2},2at} \right)$ and D as $\left( {a{t^2}, - 2at} \right)$ .
The axis of parabola is the x axis, so the other vertex is given by, C$\left( {h,0} \right)$ .
Now we can take the slope of the line AB. From the figure, $\angle BAD = 90^\circ $ as it is the angle of the square.
As the diagonal is the angle bisector of the vertex of the square, we can write,
\[ \Rightarrow \angle BAC = \angle DAC = 45^\circ \]
We can write the slope of AB as the tangent of the angle it makes with the positive x axis.
\[ \Rightarrow m = \tan \angle DAC\]
So we have,
\[ \Rightarrow m = \tan 45^\circ \]
We know that \[\tan 45^\circ = 1\] . So, we get the slope as,
\[ \Rightarrow m = 1\]
We know that slope of line joining 2 points $\left( {{x_1},{y_1}} \right)$ and $\left( {{x_2},{y_2}} \right)$ is given by,
$m = \dfrac{{{y_2} - {y_1}}}{{{x_2} - {x_1}}}$
On substituting the points A and B, we get
$ \Rightarrow m = \dfrac{{2at - 0}}{{a{t^2} - 0}}$
On simplification we get,
$ \Rightarrow m = \dfrac{{2at}}{{a{t^2}}}$
On cancelling common terms we get,
$ \Rightarrow m = \dfrac{2}{t}$
But we found the slope of AB as 1.
$ \Rightarrow 1 = \dfrac{2}{t}$
On cross multiplication we get,
$ \Rightarrow t = 2$
Now on substituting the value of t in the coordinates of B, we get,
$B\left( {a{t^2},2at} \right) = B\left( {a \times {2^2},2a \times 2} \right)$
Hence we have,
$ \Rightarrow B\left( {4a,4a} \right)$
Now on substituting the value of t in the coordinates of D, we get,
$D\left( {a{t^2}, - 2at} \right) = D\left( {a \times {2^2}, - 2a \times 2} \right)$
Hence we have,
$ \Rightarrow D\left( {4a, - 4a} \right)$
As the x coordinates of B and D are the same, from the x coordinate of C will be its double as the diagonals of a square are perpendicular bisectors of each other and equal.
$ \Rightarrow D\left( {8a,0} \right)$
Now we have all the vertices of the square and only option B matches with the vertices.

Therefore, the correct answer is option B.

Note:
The slope a line is the tangent of the angle that the line makes with the positive x axis. While calculating the slope using the points, we must take the coordinates in the same order in both numerator and denominator. We can note that, all the vertices of the square lie in the parabola except for on the x axis. So, we can check the option and eliminate option A which is a point on the y axis. We can also reject the option C by checking the slope it makes with the origin.