Question

A square is inscribed in a circle of radius 2 which touches the line \[y=1\] at \[\left( 5,1 \right)\]. One side of the square is parallel to \[y=x+3\]. If a circle is inscribed in the square, then its area will be
A. \[2\pi \]
B. \[4\pi \]
C. \[16\pi \]
D. none of the above.

Answer 1

Hint: In this problem, we are given that A square is inscribed in a circle of radius 2 which touches the line \[y=1\] at \[\left( 5,1 \right)\]. One side of the square is parallel to \[y=x+3\]. If a circle is inscribed in the square, then we have to find its area. We can draw a suitable diagram. We can then find the side of the square from which we can find the area of the square. We can then draw a circle inscribed to a square, using Pythagoras theorem, we can find the radius of the circle, then find the area of it.

Complete step by step solution:
Here we are given that A square is inscribed in a circle of radius 2 which touches the line \[y=1\] at \[\left( 5,1 \right)\]. One side of the square is parallel to \[y=x+3\]. If a circle is inscribed in the square, then we have to find its area.
We can now draw the diagram.

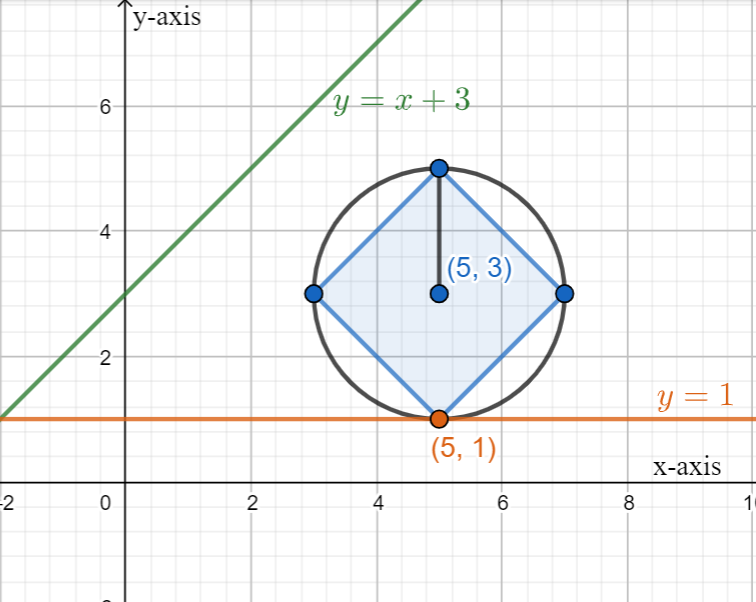
Here we can see that, we have the centre of the circle \[\left( 5,3 \right)\] and the radius will be 2 and the diameter will be 4. from the diagram.
We know that the diameter is the diagonal of the square.
We can see that,
Diameter of circle = diagonal of square = 4cm.
We know that,
Diagonal of square = \[\sqrt{2}\times side\], where we have the diagonal
\[\Rightarrow side=\dfrac{4}{\sqrt{2}}=2\sqrt{2}\]
The side of the square is \[2\sqrt{2}\]units.
We can now draw the diagram for a circle inscribed in a square.

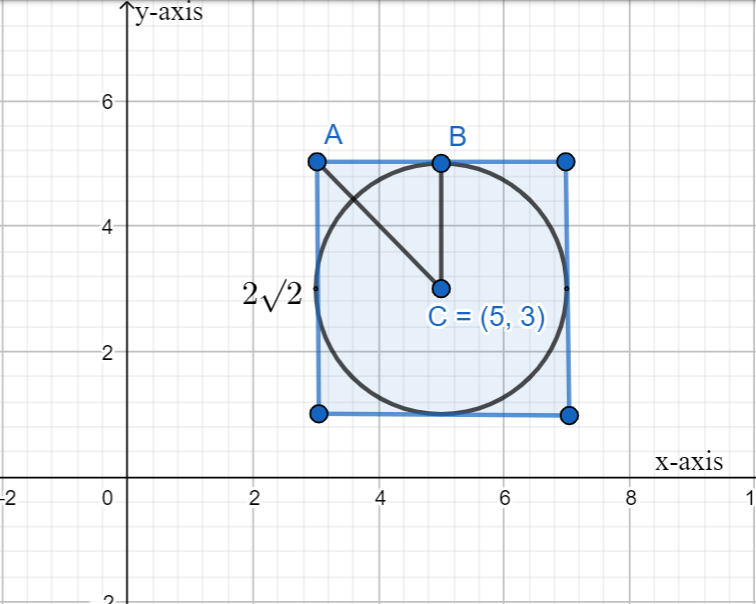
We can see that \[AB=\sqrt{2}\] as it is half the side and AC = 2 which is half of the diagonal (4 units).
We can now find the radius of the circle BC using the Pythagoras theorem.
\[\begin{align}
  & \Rightarrow B{{C}^{2}}=A{{C}^{2}}-A{{B}^{2}} \\
 & \Rightarrow B{{C}^{2}}=4-2 \\
 & \Rightarrow BC=\sqrt{2} \\
\end{align}\]
The radius of the circle is \[\sqrt{2}\]units.
We know that the area of the circle is \[\pi {{r}^{2}}\].
\[\Rightarrow \pi {{\left( \sqrt{2} \right)}^{2}}=2\pi \]
The area of the circle is \[2\pi \]sq. units.
Therefore, the answer is option A. \[2\pi \].

Note: We should always remember the measurement formulas such as the area of the circle is \[\pi {{r}^{2}}\]. We should also remember that the diagonal of the square is the diameter of the circle, when a circle is inscribed in a square or square is inscribed in a circle. We should always mention the given unit in the problem.