Question

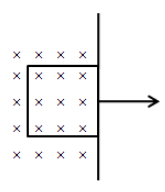
A square loop of area \[2.5 \times {10^{ - 3}}\,{{\text{m}}^2}\] and having 100 turns with a total resistance of \[100\,\Omega \] is moved out of a uniform magnetic field of 0.40T in 1 s with a constant speed. Then the work done in pulling the loop is:

A. 0
B. 1 mJ
C. \[1\,\mu \,{\text{J}}\]
D. 0.1 mJ

Answer 1

Hint: Determine the velocity of the loop after calculating the length of the loop. Calculate the emf induced in the loop using the expression for motional emf. Using Ohm’s law, calculate the current in the square loop. Use the formula for force acting on the loop when the current is flowing through it. The work done is the product of force and displacement of the loop.

Formula used:
Motional emf, \[e = NBlv\]
Here, N is the number of turns and B is the uniform magnetic field, l is the length of the loop and v is the velocity of the loop.
Force acting on the loop, \[F = N\,i\,B\,l\]
Here, i is the current in the loop.

Complete step by step answer:
We know that the work done in pulling out the square loop is the product of the force acting on the loop and the displacement of the loop. Therefore, we have to calculate the length of the loop and the force acting on the loop. We have given the area of the square loop, \[A = 2.5 \times {10^{ - 3}}\,{{\text{m}}^2}\]. Therefore, we can determine the length of the loop as,
\[l = \sqrt A \]

Substituting \[A = 2.5 \times {10^{ - 3}}\,{{\text{m}}^2}\] in the above equation, we get,
\[l = \sqrt {2.5 \times {{10}^{ - 3}}\,{{\text{m}}^2}} \]
\[ \Rightarrow l = 0.05\,{\text{m}}\]
Let’s determine the velocity of the loop as follows,
\[v = \dfrac{l}{t}\], where, t is the time.

Substituting \[l = 0.05\,{\text{m}}\] and \[t = 1\,{\text{s}}\] in the above equation, we get,
\[v = \dfrac{{0.05\,m}}{{1\,{\text{s}}}}\]
\[ \Rightarrow v = 0.05\,{\text{m/s}}\]

Now, when we pull out the square loop out of the magnetic field, the emf induces in the loop. The expression for the induced emf in the loop is,
\[e = NBlv\]
Here, N is the number of turns and B is the uniform magnetic field.
Substituting \[N = 100\], \[B = 0.4\,{\text{T}}\], \[l = 0.05\,{\text{m}}\] and \[v = 0.05\,{\text{m/s}}\] in the above equation, we get,
\[e = \left( {100} \right)\left( {0.4} \right)\left( {0.05} \right)\left( {0.05} \right)\]
\[ \Rightarrow e = 0.1\,{\text{V}}\]

Now, let’s determine the current induced in the loop using Ohm’s law as follows,
\[i = \dfrac{e}{R}\]
Here, R is the resistance of the square loop.
Substituting \[e = 0.1\,{\text{V}}\] and \[R = 100\,\Omega \] in the above equation, we get,
\[i = \dfrac{{0.1}}{{100}}\]
\[ \Rightarrow i = {10^{ - 3}}\,{\text{A}}\]

The force acting on the loop when the current flows through it is expressed as,
\[F = N\,i\,B\,l\]
Substituting \[N = 100\], \[B = 0.4\,{\text{T}}\], \[l = 0.05\,{\text{m}}\] and \[i = {10^{ - 3}}\,{\text{A}}\] in the above equation, we get,
\[F = \left( {100} \right)\left( {{{10}^{ - 3}}} \right)\left( {0.4} \right)\left( {0.05} \right)\]
\[ \Rightarrow F = 2 \times {10^{ - 3}}\,{\text{N}}\]

Now, we can determine the work done to pull out the whole square loop out of the magnetic field as,
\[W = F\,l\]
Substituting \[F = 2 \times {10^{ - 3}}\,{\text{N}}\] and \[l = 0.05\,{\text{m}}\] in the above equation, we get,
\[W = \left( {2 \times {{10}^{ - 3}}} \right)\left( {0.01} \right)\]
\[ \Rightarrow W = 0.1 \times {10^{ - 3}}\,{\text{J}}\]
\[ \therefore W = 0.1\,{\text{mJ}}\]

So, the correct answer is option D.

Note:The expression for the induced emf in the loop is \[e = - Blv\]. The negative sign indicates that the induced emf opposes the generation of this emf. It has no other physical significance and therefore, we have neglected the negative sign in the solution. Note that the work done is given as \[W = Fl\cos \theta \]. Since the force and the length of the loop are in the same direction, we can write it as \[W = F\,l\].