Question

A square of side and a uniform thickness is divided into four equal parts. If the upper right part is removed, then find the coordinates of the center of mass of the remaining part.

Answer 1

Hint : Center of mass of a body or system of a particle is defined as, a point at which the whole of the mass of the body or all the masses of a system of particles appears to be concentrated.
Apply center of mass formula,
The equation can be applied individually to each axis,
 $ \begin{align}
  & {{X}_{com}}=\dfrac{\sum\limits_{i=0}^{n}{{{m}_{i}}{{x}_{i}}}}{M}=\dfrac{{{m}_{1}}{{x}_{1}}+{{m}_{2}}{{x}_{2}}+{{m}_{3}}{{x}_{3}}+...+{{m}_{n}}{{x}_{n}}}{M} \\
 & {{Y}_{com}}=\dfrac{\sum\limits_{i=0}^{n}{{{m}_{i}}{{y}_{i}}}}{M}=\dfrac{{{m}_{1}}{{y}_{1}}+{{m}_{2}}{{y}_{2}}+{{m}_{3}}{{y}_{3}}+...+{{m}_{n}}{{y}_{n}}}{M} \\
\end{align} $
This formula is used for point objects.

Complete step by step solution:
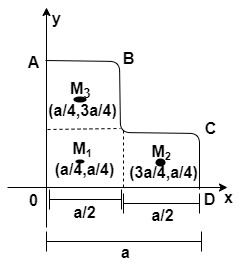
We have given, a square whose side is a. divide the square into four equal parts.
If the upper part of the square is removed. Then we left with three parts of the square. Now, we have to find the coordinates of the centre of mass of the remaining three parts. Let M is the mass of particles at each corner of the square.
Use center of mass formula,
 $ \begin{align}
  & {{M}_{1}}\left( x,y \right)=\left( \dfrac{a}{4},\dfrac{a}{4} \right) \\
 & {{M}_{2}}\left( x,y \right)=\left( \dfrac{3a}{4},\dfrac{a}{4} \right) \\
 & {{M}_{3}}\left( x,y \right)=\left( \dfrac{a}{4},\dfrac{3a}{4} \right) \\
\end{align} $
Now, center of mass formula is given by,
 $ \begin{align}
  & {{X}_{com}}=\dfrac{{{M}_{1}}{{x}_{1}}+{{M}_{2}}{{x}_{2}}+{{M}_{3}}{{x}_{3}}}{M} \\
 & {{M}_{1}}={{M}_{2}}={{M}_{3}}=M \\
 & {{X}_{com}}=\dfrac{M\left( \dfrac{a}{4} \right)+M\left( \dfrac{3a}{4} \right)+M\left( \dfrac{a}{4} \right)}{M+M+M} \\
 & {{X}_{com}}=\dfrac{\left( \dfrac{a}{4}+\dfrac{3a}{4}+\dfrac{a}{4} \right)M}{3M} \\
 & {{X}_{com}}=\dfrac{5a}{4}\times \dfrac{1}{3}=\dfrac{5a}{12} \\
 & {{Y}_{com}}=\dfrac{{{M}_{1}}{{y}_{1}}+{{M}_{2}}{{y}_{2}}+{{M}_{3}}{{y}_{3}}}{{{M}_{1}}+{{M}_{2}}+{{M}_{3}}} \\
 & {{Y}_{com}}=\dfrac{M\left( \dfrac{a}{4} \right)+M\left( \dfrac{a}{4} \right)+M\left( \dfrac{3a}{4} \right)}{M+M+M} \\
 & {{Y}_{com}}=\dfrac{\left( \dfrac{a}{4}+\dfrac{a}{4}+\dfrac{3a}{4} \right)M}{3M}=\dfrac{5a}{12} \\
\end{align} $
The coordinates of the centre of mass is $ \left( \dfrac{5a}{12},\dfrac{5a}{12} \right) $.

Note:
A point where the whole mass of the body can be assumed to be located or concentrated is called the centre of mass. The point can be real or imaginary, for example in case of a hollow or empty box the mass is physically not located at the centre of mass point. The mass is supposed to be located at the centre of mass in order to simplify calculations.