Question

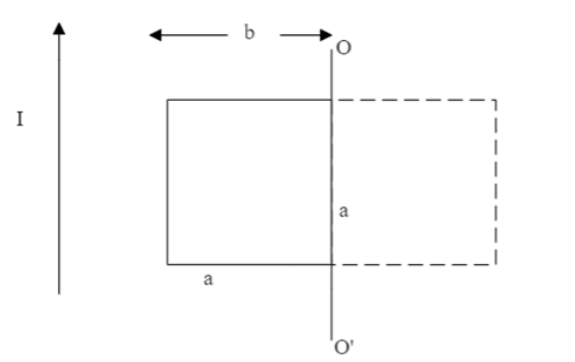
A square wire frame of side $ a $ is placed $ b $ away from a long straight conductor carrying current $ I $ . The frame has resistance $ R $ and self-inductance $ L $ . The frame is rotated by $ 180^\circ $ about $ OO' $ as shown in figure. Find the electric charge flown through the frame.

(A) $ \dfrac{{2{\mu _0}i{a^2}}}{{2\pi Rb}} $
(B) $ \dfrac{{{\mu _0}i}}{{2\pi R}}{\log _e}\dfrac{{b + a}}{{b - a}} $
(C) $ \dfrac{{{\mu _0}ia}}{{2\pi R}}{\log _e}\dfrac{{b + a}}{{b - a}} $
(D) None of these

Answer 1

Hint: We know that the faraday's law stated that a changing magnetic field produces an electric field. So charges that are free to move will cause an EMF and a current. Thus the magnetic statement of Faraday’s Law is that EMF induced in a loop is proportional to rate of change in flux.
 $ E = iR = \dfrac{{\Delta \phi }}{{\Delta t}} $
We also know that the current in a conductor is nothing but, charge flowing in it per unit time $ i = \dfrac{q}{t} $
We also know that, $ \phi = \int {B.dA} $ .

Formulas used: We will be using the formula $ E = iR = \dfrac{{\Delta \phi }}{{\Delta t}} $ where $ E $ is the EMF induced by current $ i $ , flowing through a conductor with resistance $ R $ and $ \Delta \phi $ is the change in flux of the body, while $ \Delta t $ is the change in time intervals. We will also be using, $ \phi = \int {B.dA} $ where $ B $ is the magnetic field intensity produced due to the flux and $ dA $ is the change in area.

Complete Step by Step Solution
We know that by faraday’s Laws of electromagnetism, $ E = iR = \dfrac{{\Delta \phi }}{{\Delta t}} $ we also know that $ q = it $ , Thus the charge induced on a body can be given by, $ \dfrac{{{Q_{ind}}}}{{\Delta t}}R = \dfrac{{\Delta \phi }}{{\Delta t}} $ .
 $ \Rightarrow {Q_{ind}} = \dfrac{{\Delta \phi }}{R} $ .

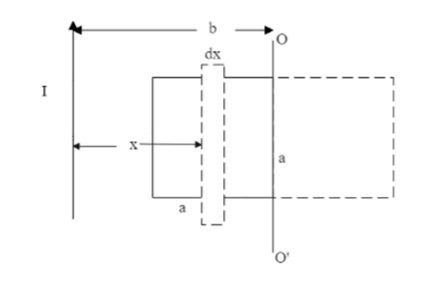
Consider a small strip of width $ dx $ at the distance of $ x $ from the current carrying wire.So let us find the change in flux by finding the final flux and initial flux.
 $ d\phi = B.dA $
Integrating the expression to find the initial and final fluxes of the thin strip
 $ \int {d\phi } = \int {B.dA} $
We know that $ \int {d\phi } = \phi $ and $ B = \dfrac{{{\mu _0}I}}{{2\pi x}} $ . Also the are of the strip will be $ A = a \times dx $ .
 Substituting the values be get,
 $ \phi = \int {\dfrac{{{\mu _0}I}}{{2\pi x}} \times adx} $
The limits can be specified to be, $ \left( {b - a} \right) $ to $ b $ .
 $ \phi = \dfrac{{{\mu _0}Ia}}{{2\pi }}\int_{b - a}^b {\dfrac{{dx}}{x}} = \dfrac{{{\mu _0}Ia}}{{2\pi }}\left[ {{{\log }_e}b - {{\log }_e}(b - a)} \right] $
 $ \Rightarrow \phi = \dfrac{{{\mu _0}Ia}}{{2\pi }}{\log _e}\left( {\dfrac{b}{{b - a}}} \right) $
Now, consider the final position to find flux for,

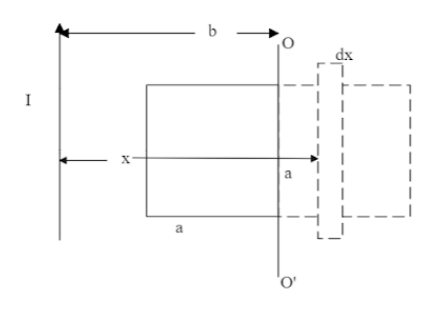
Finding flux using integration,
 $ \phi = \int {\dfrac{{{\mu _0}I}}{{2\pi x}} \times adx} $
but the limits will be $ b $ to $ b + a $ .
 $ \phi = \dfrac{{{\mu _0}Ia}}{{2\pi }}\int_b^{b + a} {\dfrac{{dx}}{x}} = \dfrac{{{\mu _0}Ia}}{{2\pi }}\left[ {{{\log }_e}(b + a) - {{\log }_e}(b)} \right] $
 $ \Rightarrow \phi = \dfrac{{{\mu _0}Ia}}{{2\pi }}{\log _e}\left( {\dfrac{{b + a}}{b}} \right) $
Now we have both the initial and final flux let us find the differences between them, $ \Delta \phi = {\phi _f} - ( - {\phi _i}) = \dfrac{{{\mu _0}Ia}}{{2\pi }}{\log _e}\left( {\dfrac{{b + a}}{b}} \right) - \dfrac{{{\mu _0}Ia}}{{2\pi }}{\log _e}\left( {\dfrac{b}{{b - a}}} \right) $
Since $ \phi = B.dA\cos \theta $ and here $ \theta = 180^\circ $
 $ \Delta \phi = \dfrac{{{\mu _0}Ia}}{{2\pi }}{\log _e}\left[ {\left( {\dfrac{{b + a}}{b}} \right) \times \left( {\dfrac{b}{{b - a}}} \right)} \right] $
 $ \Rightarrow \Delta \phi = \dfrac{{{\mu _0}Ia}}{{2\pi }}{\log _e}\left( {\dfrac{{b + a}}{{b - a}}} \right) $
Since we know that $ {Q_{ind}} = \dfrac{{\Delta \phi }}{R} $ ,
 $ Q = \dfrac{{{\mu _0}Ia}}{{2\pi R}}{\log _e}\left( {\dfrac{{b + a}}{{b - a}}} \right) $
Hence the correct answer is option C.

Note
The problem can also be solved without breaking the limits and taking , solving for, $ \phi = \dfrac{{{\mu _0}Ia}}{{2\pi }}\int_{b - a}^{b + a} {\dfrac{{dx}}{x}} = \dfrac{{{\mu _0}Ia}}{{2\pi }}\left[ {{{\log }_e}(b + a) - {{\log }_e}(b - a)} \right] $
 $ \Rightarrow \phi = \dfrac{{{\mu _0}Ia}}{{2\pi }}\left[ {{{\log }_e}(b + a) - {{\log }_e}(b - a)} \right] = \dfrac{{{\mu _0}Ia}}{{2\pi }}{\log _e}\left( {\dfrac{{b + a}}{{b - a}}} \right) $
Thus $ {Q_{ind}} $ will be, $ Q = \dfrac{{{\mu _0}Ia}}{{2\pi R}}{\log _e}\left[ {\dfrac{{b + a}}{{b - a}}} \right] $ .