Question

A standing wave pattern of amplitude A in a string of length L shows 2 nodes (plus those at two ends). If one end of the string corresponds to the origin and v is the speed of the progressive wave, the disturbance in the string could be represented (with appropriate phase) as:

\[A.\,y(x,t)=A\sin \left( \dfrac{2\pi x}{L} \right)\cos \left( \dfrac{2\pi vt}{L} \right)\]
\[B.\,y(x,t)=A\cos \left( \dfrac{3\pi x}{L} \right)\sin \left( \dfrac{3\pi vt}{L} \right)\]
\[C.\,y(x,t)=A\cos \left( \dfrac{4\pi x}{L} \right)\cos \left( \dfrac{4\pi vt}{L} \right)\]
\[D.\,y(x,t)=A\sin \left( \dfrac{3\pi x}{L} \right)\cos \left( \dfrac{3\pi vt}{L} \right)\]

Answer 1

Hint: The solution of this problem starts with the usage of the standard equation of a standing wave, and then expressing the wavelength, the angular wave number and the angular wave frequency in terms of length of the string.

Formula Used:
\[y(x,t)=A\sin \left( kx \right)\cos \left( wt \right)\]

Complete step-by-step answer:
The amplitude of a standing wave pattern = A
The length of the string = L
The total number of nodes = 2 nodes + 2 nodes at the end = 4 nodes
Therefore, the total number of nodes = 4 nodes
The speed of the progressive wave = v
A standing waveform diagram.

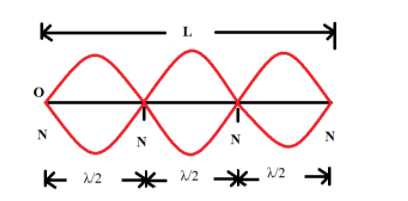
The end nodes will be present as the displacement will be zero at the both of the ends.
The nodes will be equidistant from each other. The distance between the two nodes will be \[{}^{\lambda }/{}_{2}\].
As the total number of nodes is 4, thus a total of 3 loops will be formed.

The equation of the standing wave is given by,
\[y(x,t)=A\sin \left( kx \right)\cos \left( wt \right)\] …… (1)
Where A is the amplitude of the standing wave,
k is the angular wave number denoted by \[{}^{2\pi }/{}_{\lambda }\],
w is the angular frequency denoted by \[2\pi f\].

Now we need to express the wavelength \[(\lambda )\]in terms of the length (L) and the frequency (f) in terms of the length (L) and the velocity (v) to obtain the required equation.

As the distance between the nodes is \[{}^{\lambda }/{}_{2}\], so the total distance will be,
\[\dfrac{\lambda }{2}+\dfrac{\lambda }{2}+\dfrac{\lambda }{2}=\dfrac{3\lambda }{2}\]

Therefore, the wavelength \[(\lambda )\]in terms of the length (L) of the string will be,
\[\begin{align}
  & L=\dfrac{3\lambda }{2} \\
 & \lambda =\dfrac{2L}{3} \\
\end{align}\]

As we have obtained the expression of wavelength in terms of the length, we will use the same to express the angular wave number in terms of length.
So, we get,
\[\begin{align}
  & k=\dfrac{2\pi }{\lambda } \\
 & k=\dfrac{2\pi }{{}^{2L}/{}_{3}} \\
\end{align}\]
\[k=\dfrac{3\pi }{L}\] …… (2)

The wave frequency is the ratio of the wave velocity and its wavelength, so we have,
\[f=\dfrac{v}{\lambda }\]
Substitute this wave frequency value in the expression of the angular frequency.
\[\begin{align}
  & w=2\pi f \\
 & w=\dfrac{2\pi v}{\lambda } \\
\end{align}\]
Again substitute the value of wavelength in this expression.
\[w=\dfrac{2\pi v}{{}^{2L}/{}_{3}}\]
\[w=\dfrac{3\pi v}{L}\] …… (3)
Substitute the equations (2) and (3) in (1), so we get,
\[y(x,t)=A\sin \left( \dfrac{3\pi x}{L} \right)\cos \left( \dfrac{3\pi vt}{L} \right)\]
Hence the required expression.

As, the disturbance in the string is represented by \[y(x,t)=A\sin \left( \dfrac{3\pi x}{L} \right)\cos \left( \dfrac{3\pi vt}{L} \right)\], thus option (D) is correct.

Note: The things to be on your finger-tips for further information on solving these types of problems are: The total number of nodes formation should be taken care of, as the length of the string will be calculated in terms of the number of nodes formed and even the further calculation will be dependent on the length of the string.