Question

A starts from a place P to go to a place Q. at the same time B starts from Q to P. if after meeting each other, A and B took 4 hours and 9 hours more respectively to reach their destination, what is the ratio of their speeds?
(a) 3:2
(b) 5:2
(c) 9:4
(d) 9:13

Answer 1

Hint: To solve this question, we will consider a point C’ between places P and Q where A and B meet. We will consider the distance PC as x and CQ as y. After this, we will apply the condition that at the same time A and B course different distances. Also, we will apply the condition of the remaining distances for A and Band how much time they need to cover it.

Complete step-by-step answer:
To solve this question, we will consider here a point C between the points P and Q such that the total distance between P and Q is d as shown:

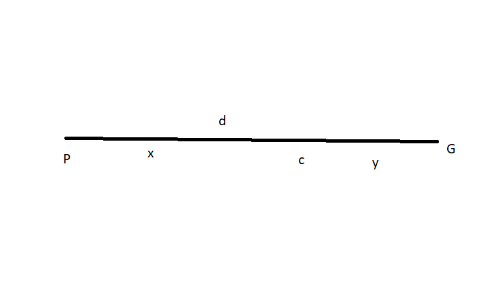
Thus, from above figure we can see that the total distance, d=x+y. therefore:
$\Rightarrow y=d-x...........(i)$
We are given that, now A and B have met at point C. it is further given that the time taken for A to go from point c to point Q is 4 hours. Let us say that the speed of A is $V_A$ then the relation between the distance travelled, velocity and time elapsed is given as
$$\begin{array}{rl}& speed={\displaystyle \frac{Totaldistance}{totaltime}}\\ & V_A=y\\ & \Rightarrow y=4V_A............(ii)\end{array}$$
Now, we are given that the time taken for B to go to point Q from point A is 9 hours. Thus, the relation between speed, distance travelled and total time taken is given by
$\begin{array}{rl}& V_B={\displaystyle \frac{x}{9}}\\ & \Rightarrow x=9V_B............(iii)\end{array}$
Where $V_B$= velocity of B
Now, we are given that, initially A takes time t and reach the point C from point P. the same time is also taken by B to reach the point C from point Q. thus, we get the following relation:
$\begin{array}{rl}& x=V_{A}t.............(iv)\\ & y=V_{B}t..............(v)\end{array}$
Now we will divide the equation (iv) by equation (v). After dividing, we will get:
$\begin{array}{rl}& {\displaystyle \frac{x}{y}}={\displaystyle \frac{V_{A}t}{V_{B}t}}\\ & \Rightarrow {\displaystyle \frac{x}{y}}={\displaystyle \frac{V_A}{V_B}}...........(vi)\end{array}$
Now, we will put the values of x and y from equation (iv) and (v) into the equation (vi). After doing this, we will get following:
$${\displaystyle \frac{9V_B}{4V_A}}={\displaystyle \frac{V_A}{V_B}}$$
$\begin{array}{rl}& \Rightarrow 9{V_B}^2=4{V_A}^2\\ & \Rightarrow 3V_B=2V_A\\ & \Rightarrow {\displaystyle \frac{V_A}{V_B}}={\displaystyle \frac{3}{2}}\end{array}$

So, the correct answer is “Option A”.

Note: Another way of doing this question is as follows when A and B meet at point C, then we can have following relation:
$$V_{A}t+V_{B}t=d$$
After meeting, the distance left for $A=V_{B}t$ and the distance left for $B=V_{A}t$. Now according to the question, $V_{B}t=V_A$. Also $V_{A}t=9V_B$. Therefore we get:
${\displaystyle \frac{V_{B}t}{V_{A}t}}={\displaystyle \frac{4V_A}{9V_B}}\Rightarrow {\displaystyle \frac{V_A}{V_B}}={\displaystyle \frac{3}{2}}$