Question

A stone is tied to a weightless string and revolves in a vertical circle of radius 5m. (1) What should be the minimum speed of the stone at the highest point of the circle so that the string doesn’t slack? (2) What should be the speed of the stone at the lowest point in this situation?

Answer 1

Hint: As a first step, you could consider the highest and the lowest point on the vertical circular motion. You could then balance all the forces acting on the stone. Rearranging the terms and substituting accordingly will give you the velocity at the highest point. Then you could use the law of conservation of energy to find the velocity at the lowest point.

Complete Step by step solution:
In the question, we are given a stone that is tied to some weightless string that is being revolved in a vertical circle of radius 5m. Then we have two sub questions to be solved. One is about the minimum speed of stone at highest point and the other is about the speed of stone at lowest point.

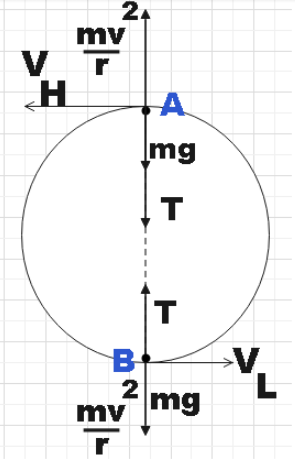
(1) For the highest point in the circular motion:
The forces acting on the stone can be balanced to get,
$T+mg=\dfrac{m{{v}_{H}}^{2}}{r}$

For minimum velocity at this point, the tension in the string at this point will be zero. Thus we get,
$\dfrac{m{{v}_{H}}^{2}}{r}=mg$
$\Rightarrow {{v}_{H}}\ge \sqrt{rg}$

Substituting the values,
$\Rightarrow {{v}_{H}}\ge \sqrt{5\times 9.8}$
$\therefore {{v}_{H}}\ge 7m{{s}^{-1}}$

Therefore, we have found that the velocity at the highest point to be $7m/s$.

(2) For the lowest point in the circular motion,
By law of conservation of energy at the highest and lowest points will be the same.
${{E}_{A}}={{E}_{B}}$
$\Rightarrow \dfrac{1}{2}m{{v}_{L}}^{2}=\dfrac{1}{2}m{{v}_{H}}^{2}+mg\left( 2r \right)$
$\Rightarrow \dfrac{1}{2}m{{v}_{L}}^{2}=\dfrac{1}{2}m\left( rg \right)+mg\left( 2r \right)$
$\Rightarrow {{v}_{L}}=\sqrt{5rg}$

Substituting the given values,
${{v}_{L}}=\sqrt{5\times 5\times 9.8}$
$\therefore {{v}_{L}}=7\sqrt{5}m{{s}^{-1}}$

Therefore, we found the velocity at the lowest point to be $7\sqrt{5}m/s$.

Note:
You may have noted that we have taken the direction of revolution of the stone to be in anti clockwise direction. The direction chosen is actually arbitrary and you may also choose it to be clockwise. This direction actually has no effect in the solution, so we shouldn’t bother about it much.