
A suspended simple pendulum of length
Answer
404.4k+ views
Hint: The mass is attached to an inextensible string and suspended from the fixed support. It is called a simple pendulum. To solve the given problem, consider the positions of the pendulum that is held.
Formula used:
Where,
Complete step by step answer:
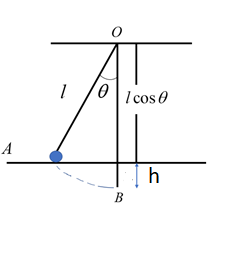
Calculate the height of the pendulum. We can consider
The height of the pendulum can be calculated as,
Substituting the values of the
Take out
Therefore the height of the pendulum is
The velocity of the pendulum released at the lowest point means the velocity of the pendulum when released from
Consider kinetic energy at
Kinetic energy at
Where,
Cancel out the common terms in the equation.
Taking the left-hand side
Substitute the value of the height in the equation.
To remove the square on the left-hand side, take the square root on the right-hand side. We get,
Therefore, the value of the simple pendulum on releasing, its velocity at the lowest points will be,
So, the correct answer is “Option C”.
Note:
The pendulum will have one mean position and two extreme positions. At the mean position, the energy of the pendulum is kinetic. At the two extreme positions, the energy of the pendulum is potential. And in between the extreme and mean position the energy is potential plus kinetic.
Formula used:
Where,
Complete step by step answer:

Calculate the height of the pendulum. We can consider
The height of the pendulum can be calculated as,
Substituting the values of the
Take out
Therefore the height of the pendulum is
The velocity of the pendulum released at the lowest point means the velocity of the pendulum when released from
Consider kinetic energy at
Kinetic energy at
Where,
Cancel out the common terms in the equation.
Taking the left-hand side
Substitute the value of the height in the equation.
To remove the square on the left-hand side, take the square root on the right-hand side. We get,
Therefore, the value of the simple pendulum on releasing, its velocity at the lowest points will be,
So, the correct answer is “Option C”.
Note:
The pendulum will have one mean position and two extreme positions. At the mean position, the energy of the pendulum is kinetic. At the two extreme positions, the energy of the pendulum is potential. And in between the extreme and mean position the energy is potential plus kinetic.
Recently Updated Pages
Express the following as a fraction and simplify a class 7 maths CBSE

The length and width of a rectangle are in ratio of class 7 maths CBSE

The ratio of the income to the expenditure of a family class 7 maths CBSE

How do you write 025 million in scientific notatio class 7 maths CBSE

How do you convert 295 meters per second to kilometers class 7 maths CBSE

Write the following in Roman numerals 25819 class 7 maths CBSE

Trending doubts
State and prove Bernoullis theorem class 11 physics CBSE

What are Quantum numbers Explain the quantum number class 11 chemistry CBSE

Write the differences between monocot plants and dicot class 11 biology CBSE

Who built the Grand Trunk Road AChandragupta Maurya class 11 social science CBSE

1 ton equals to A 100 kg B 1000 kg C 10 kg D 10000 class 11 physics CBSE

State the laws of reflection of light




