Question

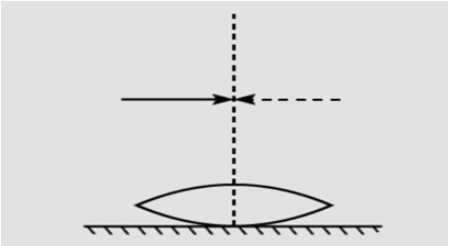
A symmetric biconvex lens of radius of curvature R and made of glass of refractive index 1.5 is placed on a layer of liquid placed on top of a plane mirror as shown in the figure. An optical needle with its tip on the principal axis of the lens is moved along the axis until its real, inverted image coincides with the needle itself. The distance of the needle from the lens is measured to be x. On removing the liquid layer and repeating the experiment the distance is found to be y. obtain the expression for the refractive index of the liquid in terms of x and y.

Answer 1

Hint- The formula that gives the relationship between the focal length, refractive index and the radii of the curvature is known as the Lens maker formula.

Formula used:
*We have the formula for the combination of two lenses as follows.
                           $\dfrac{1}{f} = \dfrac{1}{{{f_1}}} + \dfrac{1}{{{f_2}}}$
*Lens maker’s formula is given below.
$\dfrac{1}{f} = \left( {n - 1} \right)\left( {\dfrac{1}{{{R_1}}} - \dfrac{1}{{{R_2}}}} \right)$; Where n is refractive index and other symbols have their usual meaning.

Complete step by step answer:
When a symmetric biconvex lens is placed on a layer of liquid placed on top of a plane mirror, then this whole system becomes a combination of convex lens of glass and Plano concave lens of liquid. Let f is the focal length of a combination, ${f_1}$ is the focal length of a convex lens and ${f_2}$ is the focal length of a Plano concave lens of liquid.
Given in the question, for the first measurement, focal length of combination is, f=x and for second measurement focal length of convex lens is ${f_1}$ =y.
Now, for the image to coincide with the needle, ray needs to be normal to the plane mirror that means rays must come from infinity.
Let us use the formula of lens combination$\dfrac{1}{f} = \dfrac{1}{{{f_1}}} + \dfrac{1}{{{f_2}}}$.
$\dfrac{1}{x} = \dfrac{1}{y} + \dfrac{1}{{{f_2}}}$
Let us solve the above expression.
$\dfrac{1}{{{f_2}}} = \dfrac{1}{x} - \dfrac{1}{y}$
On further solving we get the following.
${f_2} = \dfrac{{xy}}{{y - x}}$ (1)
Now, let us obtain the refractive index of liquid in terms of x and y as follows.
We have the lens maker’s formula $\dfrac{1}{f} = \left( {n - 1} \right)\left( {\dfrac{1}{{{R_1}}} - \dfrac{1}{{{R_2}}}} \right)$
Now let us write the above formula for the Plano concave lens of liquid.
$\dfrac{1}{{{f_2}}} = \left( {n - 1} \right)\left( {\dfrac{1}{{{R_1}}} - \dfrac{1}{{{R_2}}}} \right)$
Here${R_1} = - R,{R_2} = \infty $, let us substitute these values in the above equation.
$\dfrac{1}{{{f_2}}} = \left( {n - 1} \right)\left( {\dfrac{1}{{ - R}} - \dfrac{1}{\infty }} \right)$
Let us further solve this expression.
$\dfrac{1}{{{f_2}}} = \left( {n - 1} \right)\left( {\dfrac{1}{{ - R}}} \right)$
Now, let us use the equation (1) and above expression becomes,
$\dfrac{{y - x}}{{xy}} = \left( {n - 1} \right)\left( {\dfrac{1}{{ - R}}} \right)$
Let us further simplify and find the value of the refractive index.
$n = 1 - \dfrac{{R\left( {y - x} \right)}}{{xy}}$ (2)
Now let us write the lens makers formula for convex lenses.
Let us substitute these values ${R_1} = R,{R_2} = - R,n = 1.5$ in $\dfrac{1}{f} = \left( {n - 1} \right)\left( {\dfrac{1}{{{R_1}}} - \dfrac{1}{{{R_2}}}} \right)$.
$\dfrac{1}{y} = \left( {1.5 - 1} \right)\left( {\dfrac{1}{R} + \dfrac{1}{R}} \right)$
Let us simplify the above expression.
$\dfrac{1}{y} = 0.5 \times \dfrac{2}{R} \Rightarrow R = y$ (3)
Now, let us substitute the value from equation (3) to equation (2).
$n = 1 - \dfrac{{y\left( {y - x} \right)}}{{xy}}$
Let us simplify the above expression.
$n = \dfrac{{xy - y\left( {y - x} \right)}}{{xy}} \Rightarrow n = \dfrac{{2x - y}}{{xy}}$
Hence, the refractive index in terms of x and y is $\dfrac{{2x - y}}{{xy}}$.

Note:
*Plano concave lens is a lens having one concave surface and one plane surface and negative focal length.
*Biconvex lenses are used as magnifying lenses.