Question

A tangent galvanometer has a coil of 25 turns and a radius of 15 cm. The horizontal component of the earth's magnetic field is $3 \times 10^{-5}$T. The current required to produce a deflection of $45^{\circ}$ in it is
A. 0.14 A
B. 0.29 A
C. 1.2 A
D. $3.6 \times 10^{-5}$ A

Answer 1

Hint: A galvanometer is a device that detects current flow in a circuit. A tangent galvanometer employs the principle of the magnetic effect of current. The deflection is due to the magnetic field that the current will create and due to the earth’s magnetic field.

Complete step-by-step solution:
A tangent galvanometer follows tangent law as in parallelogram vector addition. It consists of a coil which generates a magnetic field in the center due to the current passing in it.
The magnetic field inside the galvanometer due to the coil is:
$B = \dfrac{\mu_0 n i}{2r}$
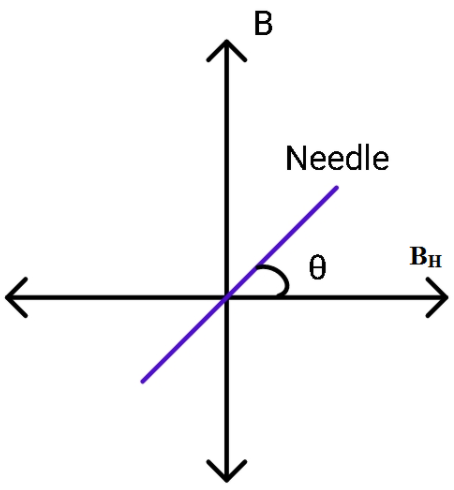
There is also an external magnetic field acting on the coil due to the horizontal component of Earth's magnetic field. These fields are perpendicular to each other. Therefore any deflection of angle $\theta$ will be due to these fields. The relation between the two fields is:
$B = B_H \tan \theta$
Where $B_H$ is the horizontal component of the earth's magnetic field.

Equating the two expressions of the magnetic field, we get:
$B_H \tan \theta = \dfrac{\mu_0 n i}{2r}$
We are given the magnetic field $B_H = 3 \times 10^{-5}$T, the deflection $\theta = 45^{\circ}$, number of turns n= 25 and the radius r= 0.15 cm and we need to find the current in the circuit with the help of this expression.
We find
$B_H \tan \theta = 3 \times 10^{-5} \times 1$ T
Therefore, the current will be:
$ i = \dfrac{2 \times 0.15 \times 3 \times 10^{-5} }{1.25 \times 10^{-6} \times 25}$
$i = 0.2864$A
Therefore, the correct answer is an option (B).

Note: The direction of the earth’s magnetic field is perpendicular to the direction of the magnetic field produced by the coil. The coil is just like a solenoid one can apply the right-hand thumb rule around the wire of the coil to obtain the direction of the magnetic field. But the simplest way is to remember the case of the solenoid.