Question

A tank with rectangular box and rectangular sides,open at the top is to be constructed so that its depth is 2m and volume is $8{m^3}$. If the building of a tank costs Rs.70 per sq metres for the base and RS.45 per square metre for sides, what is the cost of the least expensive tank?

Answer 1

Hint: Make use of the formula of volume of a cuboid and solve this.

Complete step-by-step answer:
Let us first construct a figure with the data given
 

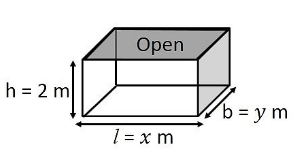
Let us consider the length of the box to be= x metres and
The Breadth of the tank be= y metres
The height of the tank is given as =h metres
Volume of the tank is also given as 8cubic metres
The formula for the volume of the tank=$l \times b \times h$
$
   \Rightarrow 8 = 2 \times x \times y \\
   \Rightarrow 4 = xy \\
   \Rightarrow y = \dfrac{4}{x} - - - - - - - - (i) \\
 $
Given: Building a tank costs Rs.70 per sq.meter for base
Area of base=$l \times b$
Area of base=xy
Cost of base=70(xy)
Also given cost is Rs.45 per square metre
Area of closed sides=2(hl+hb)
                                 =2(2x+2y)
                          =4(x+y)
Cost of making sides =45[4(x+y)]=180(x+y)
Let C be the total cost of tank
C(x)=Cost of Base+Cost of sides
C(x)=70(xy)+180(x+y)
We got the value of $y = \dfrac{4}{x}$ from eq (i)
Let’s substitute the value here, so we get
C(x)=70(4)+$180\left( {x + \dfrac{4}{x}} \right)$
C(x)=280+180$(x + 4{x^{ - 1}})$
We need to minimise the cost of the tank
So, let's find out the minimum of this
So, we will differentiate C(x) with respect to x
So, we get $C'(x) = \dfrac{{d(280 + 180(x + 4{x^{ - 1}}))}}{{dx}}$
\[\
  C'(x) = 0 + 180(1 + ( - 1)4{x^{ - 1 - 1}} \\
  C'(x) = 180(1 - 4{x^{ - 2}}) \\
  C'(x) = 180(1 - \dfrac{4}{{{x^2}}}) \\
 \]
Putting C’(x)=0,
(x-2)(x+2)=0
So, x=2 or x=-2
Since length cannot be negative , the value of x=2
Finding $
  {C^{''}}(x) \\
    \\
$ ,
Differentiating $C'(x)$ with respect to x, we get
${C^{''}}(x) = \dfrac{{1440}}{{{x^3}}}$
From this, we get $x=2$ is a point of minima
Thus, the least cost of construction
$C(x)=280+180\left( {2 + \dfrac{4}{2}} \right)$
From this we get $280 +720=1000$
So, from this we get the least cost of construction to be equal to Rs.1000.

Note: Whenever we have to find the minima, we have to find out the second order derivative and then find out the least cost. One should be careful while differentiating.