Question

A thin prism ${{P}_{1}}$ with angle 4° and made from glass of refractive index 1.54 is combined with another prism ${{P}_{2}}$ made from glass of refractive index 1.72 to produce dispersion without deviation. The angle of prism ${{P}_{2}}$ is:
A. 5.33°
B. 4°
C. 3°
D. 2.6°

Answer 1

Hint: Recall the expression for minimum deviation in thin prisms or else you derive the same by considering the case of passage of light through a triangular prism and applying basic geometry and using Snell’s law. Also, in the given question we are discussing the combination of two such prisms such that their combination results in zero deviation. That is deviation caused by one is the negative of the other. Now you could substitute the above expression in this condition to get the required quantity.

Formula used: Expression for minimum deviation,
${{\delta }_{m}}=\left( {{n}_{21}}-1 \right)A$

Complete step by step answer:
In the question we are given two prisms of different refractive indices as well as different prism angles. They are combined such that they produce dispersion without deviation. We are given refractive indices of both prisms and also angle of one prism and with that we are asked to find the angle of prism of the other.
Let us first derive the expression relating the angle of prism (A) and deviation (δ).

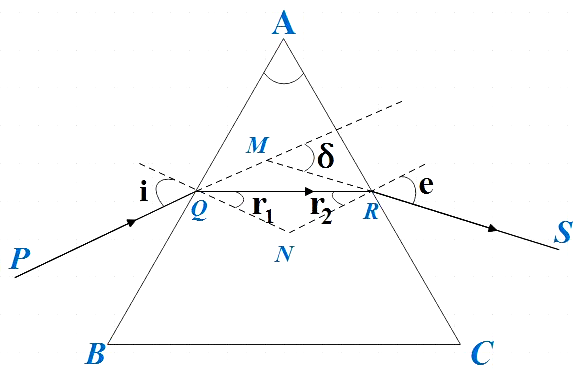
This is what happens for a light ray when it passes through a prism. It suffers from refraction at two faces of the prism. At the first face (air to glass), angle of incidence and angle of refraction are $i$ and ${{r}_{1}}$ respectively. At the second face (glass to air), the angle of incidence and angle of emergence are ${{r}_{2}}$ and $e$ respectively. Angle made by the emergent ray with the direction of incident ray PQ is the angle of deviation. So basically, angle of deviation is the angle between the path the ray might have taken in the absence of prism and the path it has taken in the presence of prism.
In quadrilateral AQNR,
$\angle A+\angle QNR=180{}^\circ $ ………………………………. (1)
In triangle QNR,
${{r}_{1}}+{{r}_{2}}+\angle QNR=180{}^\circ $ …………………………….. (2)
From (1) and (2)
$\Rightarrow {{r}_{1}}+{{r}_{2}}=A$ …………………………….. (3)
We can now express the total deviation δ as the sum of the deviations at two faces.
$\delta =\left( i-{{r}_{1}} \right)+\left( e-{{r}_{2}} \right)$
$\Rightarrow \delta =i+e-A$ ……………………………. (4)
Let ${{\delta }_{m}}$ be the minimum deviation, then at ${{\delta }_{m}}$ refracted ray inside the prism is parallel to the base of prism, that is,
$\Rightarrow i=e$
$\Rightarrow {{r}_{1}}={{r}_{2}}$
Now (3) becomes,
$2r=A$
$\Rightarrow r=\dfrac{A}{2}$ ………………………… (5)
Also, (4) becomes,
${{\delta }_{m}}=2i-A$
$\Rightarrow i=\dfrac{\left( A+{{\delta }_{m}} \right)}{2}$ ……………………………….. (6)
From Snell’s law,
${{n}_{1}}\sin {{\theta }_{1}}={{n}_{2}}\sin {{\theta }_{2}}$
$\Rightarrow {{n}_{1}}\sin i={{n}_{2}}\sin r$
From (5) and (6),
$\Rightarrow {{n}_{21}}=\dfrac{{{n}_{2}}}{{{n}_{1}}}=\dfrac{\sin \left( \dfrac{A+{{\delta }_{m}}}{2} \right)}{\sin \left( \dfrac{A}{2} \right)}$ ……………………….. (7)
For a prism with a small angle of prism, that is, for a thin prism, ${{\delta }_{m}}$ is also very small. For a small angle θ,
$\sin \theta \approx \theta $
Now (7) becomes,
${{n}_{21}}=\dfrac{\left( \dfrac{A+{{\delta }_{m}}}{2} \right)}{\dfrac{A}{2}}$
$\Rightarrow {{\delta }_{m}}=\left( {{n}_{21}}-1 \right)A$ ……………………………. (8)
Now let us go back to the question.

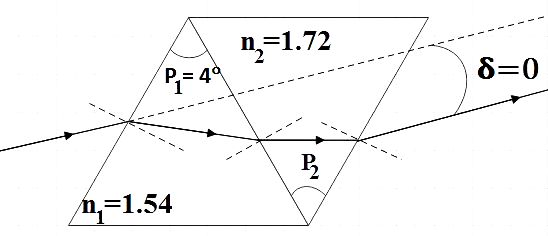
Here, the combination results in zero deviation. That is, the sum of the deviations caused by individual prisms is zero.
$\delta ={{\delta }_{1}}+{{\delta }_{2}}=0$
$\Rightarrow {{\delta }_{1}}=-{{\delta }_{2}}$ …………………………. (9)
But we have,
$\delta =\left( n-1 \right)A$
Where, δ is the deviation, n is the refractive index and A is the angle of the prism.
For the first prism,
${{\delta }_{1}}=\left( {{n}_{1}}-1 \right){{P}_{1}}$ …………………….. (10)
For the second prism,
${{\delta }_{2}}=\left( {{n}_{2}}-1 \right){{P}_{2}}$ ………………………… (11)
Substituting (10) and (11) in (9), we get,
$\left( {{n}_{1}}-1 \right){{P}_{1}}=\left( {{n}_{2}}-1 \right){{P}_{2}}$
But we are given,
${{n}_{1}}=1.54$
${{n}_{2}}=1.72$
${{P}_{1}}=4{}^\circ $
$\Rightarrow \left( 1.54-1 \right)4=\left( 1.72-1 \right){{P}_{2}}$
$\Rightarrow {{P}_{2}}=\dfrac{\left( 0.54 \right)}{\left( 0.72 \right)}\times 4=\dfrac{3}{4}\times 4$
$\Rightarrow {{P}_{2}}=3{}^\circ $
Therefore, the angle of prism ${{P}_{2}}$ is 3°.

So, the correct answer is “Option C”.

Note: You may have noticed that we have avoided the negative sign in (9) while solving the problem. This is because the negative sign simply is the indication of the fact that the deviation caused by one prism is in the opposite direction to that caused by the other. But the magnitude of deviation caused is the same for both the prisms and hence their combination results in zero deviation.