Question

A thin rod of mass $m$ and length $l$ is suspended from one of its ends. It is set into oscillation about a horizontal axis. Its angular speed is $\omega $ while passing through its mean position. How high will its centre of mass rise from its lowest position?

Answer 1

Hint: In order to solve this question, we need to use the energy conservation principle. The total mechanical energy of the system will always be conserved for the two instants given in the question. The law of conservation of energy states that the total mechanical energy of a system always remains conserved.

Complete step by step answer:
Given,
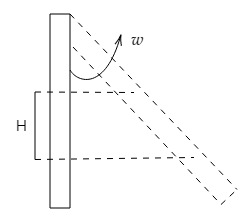
Mass of the rod $ = m$
Length of the rod $ = l$
Angular velocity $ = \omega $
In this question, we can clearly see that the exchange of energy takes places. At some point, the kinetic energy is converted into potential energy and at some other point, potential energy is converted into kinetic energy.
According to the law of conservation of energy,
Kinetic energy $ = $ Potential energy
$\dfrac{1}{2}m{v^2} = mgh$
Where,
$m$ is the mass of the rod
$v$ is the velocity of the rod
$g$ is the acceleration due to gravity
$h$ is the height attained by the rod
On further solving, we get,
$\dfrac{1}{2}{v^2} = gh$
$h = \dfrac{{{v^2}}}{{2g}}.....(1)$
On putting $v = \dfrac{{\omega L}}{2}$ in equation (1),
$h = {\left( {\dfrac{{\omega L}}{2}} \right)^2} \times \dfrac{1}{{2g}}$
$h = \dfrac{{{\omega ^2}{L^2}}}{4} \times \dfrac{1}{{2g}}$
$h = \dfrac{{{\omega ^2}{L^2}}}{{8g}}$
$h = \dfrac{{{\omega ^2}{L^2}}}{{8g}}$
So, the height at which the centre of mass will rise from the lowest position is $h = \dfrac{{{\omega ^2}{L^2}}}{{8g}}$.

Note:The motion of the centre of mass of any system of particles is always independent of the internal forces acting on it. The centre of mass moves in a way that the whole mass of the system is concentrated at that point and the external force is acting on only that single point.