Question

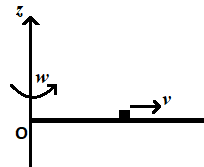
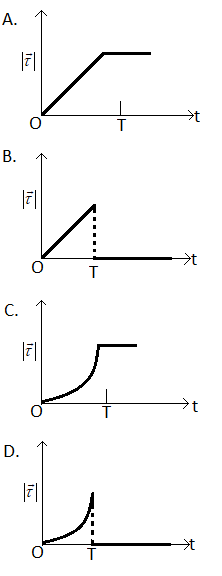
A thin uniform rod, pivoted at O, is rotating in the horizontal plane with constant angular speed \[\omega \], as shown in the figure. At time t = 0, a small insect starts from O and moves with constant speed v with respect to the rod towards the other end. It reaches the end of the rod at t = T and stops. The angular speed of the system remains $\omega $ throughout. The magnitude of the torque $\left| {\vec{\tau }} \right|$ on the system about O, as a function of time is best represented by which plot?

Answer 1

Hint: We have a uniform rod which is rotating in the horizontal plane with an angular speed ‘$\omega $’. We know that the magnitude of torque is the rate of change of angular momentum. In this case the moment of inertia is the sum of the moment of inertia of the rod and the insect. Thus we will get the angular momentum and by differentiating it we will get the magnitude of torque. Thus we will get the relation between torque and time, thus we will get the plot.

Formula used:
$\left| {\vec{\tau }} \right|=\left| \dfrac{dL}{dt} \right|$
$L=I\omega $

Complete step by step answer:
In the question we are given a rod which is pivoted at O as shown in the figure. The rod is rotating in the horizontal plane with constant angular speed ‘$\omega $’.
It is said that at a time t = 0, a small insect starts from the point O and starts moving with a velocity ‘v’ with respect to the rod towards the end and reaches the end of the rod at a time t = T.
It is also said that the angular speed of the system ‘$\omega $’ remains the same throughout.
We know that torque is the rate of change of angular momentum, i.e.
$\left| {\vec{\tau }} \right|=\left| \dfrac{dL}{dt} \right|$, were ‘$\left| {\vec{\tau }} \right|$’ is the magnitude of torque, ‘$L$’ is the angular momentum.
We know that the angular momentum is given by the equation,
$L=I\omega $, where ‘$I$’ is the moment of inertia and ‘$\omega $’ is the angular speed.
In this case the moment of inertia is the sum of the moment of inertia of the rod and the insect.
We know that the moment of inertia of the rod about the end is,
${{I}_{r}}=\dfrac{1}{3}M{{L}^{2}}$, were ‘M’ is the mass of the rod and ‘L’ is its length.
And the moment of inertia of the insect can be given as,
${{I}_{i}}=m{{x}^{2}}$, where ‘m’ is the mass of the insect and ‘x’ is the distance where the insect may be present at an arbitrary time.
Therefore we get the angular momentum as,
\[\Rightarrow L=\left( \dfrac{1}{3}M{{L}^{2}}+m{{x}^{2}} \right)\omega \]
Since $\left| {\vec{\tau }} \right|=\left| \dfrac{dL}{dt} \right|$, we need to differentiate angular momentum with respect to time.
Thus we get,
$\Rightarrow \dfrac{dL}{dt}=\dfrac{d\left( \left( \dfrac{1}{3}M{{L}^{2}}+m{{x}^{2}} \right)\omega \right)}{dt}$
We know that the angular momentum of the rod is a constant. Therefore by differentiating we get,
$\Rightarrow \dfrac{dL}{dt}=0+2mx\dfrac{dx}{dt}\omega $
We know that $\dfrac{dx}{dt}=v$ and the distance $x=v\times t$. By substituting these in the equation, we get
$\Rightarrow \dfrac{dL}{dt}=2mvt\times v\omega $
$\Rightarrow \dfrac{dL}{dt}=2m{{v}^{2}}t\omega $
Therefore we get the magnitude of torque as,
$\Rightarrow \left| {\vec{\tau }} \right|=2m{{v}^{2}}\omega t$
From this equation we can see that the magnitude of torque is directly proportional to time,
$\left| {\vec{\tau }} \right|\propto t$, i.e. torque will increase linearly with respect to time.
Therefore the correct plot of the torque is,

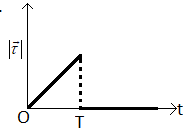
Hence the correct answer is option B.

Note:
Torque is simply the measure of force that causes the object to rotate about an axis. Thus torque cases angular acceleration in rotational motion.
Angular acceleration or rotational acceleration is the rate of change of angular velocity with respect to time of the motion of the object.
Angular momentum is a vector quantity (a quantity with both direction and magnitude) which measures the rotational momentum of a rotating body. It is the product of the angular velocity of an object and its moment of inertia with respect to the axis of rotation.