Question

A thin uniform spherical shell of mass M and radius R is held fixed. There is a small hole punched in the shell. A particle of mass m is released from rest at a distance R from the hole along a line that passes through the hole and also through the centre of the shell. The particle starts moving towards the centre of the shell only due to gravitational attraction. Find the time taken by the particle to reach the diagonally opposite end of the shell.

Answer 1

Hint: When some amount of work is done against the conservative force then the work done will be stored in the system as the potential energy as energy can neither be created nor destroyed. Along the direction of conservative force then potential energy of the system decreases. By using these two principles we will solve the question.
Formula used:
$\eqalign{
  & P.{E_i} + K.{E_i} = P.{E_f} + K.{E_f} \cr
  & P.E = \dfrac{{ - GMm}}{r} \cr
  & K.E = \dfrac{1}{2}m{v^2} \cr} $

Complete answer:
Since the mass is only acted upon the gravitational force, and gravitational force is conservative in nature, according to conservation of mechanical energy, total mechanical energy of the system is always conserved as long as only conservative forces acting on it.
That means change in mechanical energy is zero and mechanical energy(ME) will be constant always. Mechanical energy is the sum of potential and kinetic energy
$\eqalign{
  & ME = {\text{ constant}} \cr
  & \Rightarrow KE + PE = {\text{constant}} \cr
  & \therefore P.{E_i} + K.{E_i} = P.{E_f} + K.{E_f} \cr} $
Now due to gravitational force acting, the potential of the mass(m) due to gravitational force of attraction between shell of mass(M) and when distance between them is ‘r’ is given by
$P.E = \dfrac{{ - GMm}}{r}$ where ‘G’ is gravitational constant
Kinetic energy of mass m is given by
$K.E = \dfrac{1}{2}m{v^2}$
Where ‘m’ is the mass of the block and ‘v’ is the velocity of the block.
From the diagram below we will conserve energy between initial point and surface point to get velocity of mass ‘m’ at the shell surface.

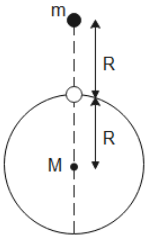
Here point at height ‘R’ from the surface is initial point and surface point is final point
$\eqalign{
  & P.{E_i} + K.{E_i} = P.{E_f} + K.{E_f} \cr
  & \Rightarrow \dfrac{{ - GMm}}{{2R}} + \dfrac{1}{2}m{v^2} = \dfrac{{ - GMm}}{R} \cr
  & \therefore v = \sqrt {\dfrac{{GM}}{R}} \cr} $
Now this velocity will be constant till mass reaches a diametrically opposite point because there will be no force acting on it inside the shell. So the time taken will be
$\eqalign{
  & s = vt \cr
  & \Rightarrow 2R = vt \cr
  & \Rightarrow \dfrac{{2R}}{v} = t \cr
  & \therefore t = 2\sqrt {\dfrac{{{R^3}}}{{GM}}} \cr} $
Hence the time taken will be $2\sqrt {\dfrac{{{R^3}}}{{GM}}} $ to reach the opposite end.

Note:
Inside the shell there will be no mass. When there is no mass then there will be no gravitational field produced. If we consider a uniform sphere where mass is uniformly distributed throughout the volume and we make a hole exactly at the center then if we take any point in that cavity, the gravitational field will be zero.