Question

A toroid has a non-ferromagnetic core of inner radius 25 cm and outer radius 26 cm around which 3500 turns of wire are wound. If the current in the wire is 11 A, find the magnetic field
(a) outside the toroid,
(b) inside the core of the toroid and
(c) in the empty space surrounded by the toroid.

Answer 1

Hint: Ampere’s law implies that the magnetic field at any point is proportional to the current enclosed in the loop. At a point outside the toroid, the current through the wire will have opposite directions at the top of the loop where the current seems to be going into the plane and at the bottom of the loop where the current seems to be coming out of the plane whereas, in the empty space, no current exists.

Formulas used:
The magnetic field inside the core of the toroid is given by, $B = \dfrac{{{\mu _0}NI}}{l}$ where ${\mu _0}$ is the permeability of free space, $N$ is the number of turns on the toroid, $I$ is the current through the wire and $l$ is the length of the wire.

Complete step by step solution:
Step 1: Sketch a diagram of the toroid and list the parameters provided in the question.

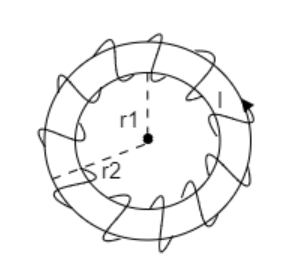
The inner radius of the toroid is ${r_1} = 25{\text{cm}}$ and its outer radius is ${r_2} = 26{\text{cm}}$
A current of $I = 11{\text{A}}$ passes through the wire wound around the toroid.
The number of turns on the toroid is $N = 3500$ .
Step 2: Find the length of the wire.
Let $l$ be the length of the wire. The length of the wire will be equal to the circumference of the toroid.
i.e., The length of the wire is given by, $l = 2\pi \left( {\dfrac{{{r_1} + {r_2}}}{2}} \right)$
Substituting for ${r_1} = 25{\text{cm}}$ and ${r_2} = 26{\text{cm}}$ in the above relation we get, $l = 2\pi \left( {\dfrac{{25 + 26}}{2}} \right) = 51\pi {\text{cm}}$
$\therefore $ the length of the wire is $l = 51\pi {\text{cm}}$ .
Step 3: Find the magnetic field (a) outside the toroid.

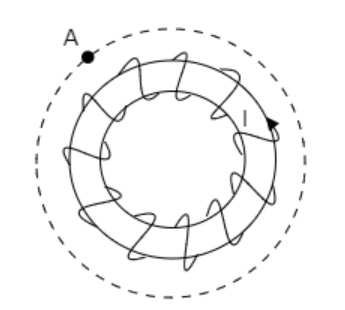
In the above figure, A is a point outside the toroid. An Amperian loop is drawn with A as a point on the loop. We observe that the current coming out of the plane gets cancelled by the current going into the plane. Thus the net current enclosed by the Amperian loop will be zero.
By Ampere’s law, the magnetic field at A will be zero.
So, the magnetic field outside the toroid is zero.
Step 4: Find the magnetic field (b) inside the core of the toroid.
The magnetic field inside the core of the toroid is given by, $B = \dfrac{{{\mu _0}NI}}{l}$ ----------- (1)
Substituting the values for the permeability of free space ${\mu _0} = 4\pi \times {10^{ - 7}}{\text{H/m}}$, $N = 3500$ , $I = 11{\text{A}}$ and $l = 51\pi {\text{cm}}$ in equation (1) we get, $B = \dfrac{{4\pi \times {{10}^{ - 7}} \times 3500 \times 11}}{{0.51\pi }} = 3.02 \times {10^{ - 2}}{\text{T}}$
$\therefore $ the magnetic field inside the core of the toroid is $B = 3.02 \times {10^{ - 2}}{\text{T}}$ .
Step 5: Find the magnetic field (c) in the empty space surrounded by the toroid.

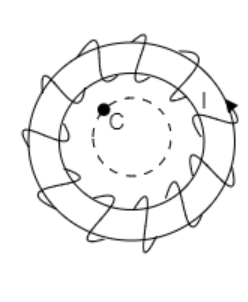
In the above figure, C is a point in the empty space surrounded by the toroid. An Amperian loop is drawn with C as a point on the loop. The loop does not enclose any current. Then by Ampere’s law, the magnetic field at C will also be zero.

Hence, the magnetic field in the empty space surrounded by the toroid is zero.

Note:
Ampere’s law states that the line integral of the magnetic field $B$ is equal to ${\mu _0}$ times the current enclosed by the Amperian loop i.e., $\oint {B \cdot dl = {\mu _0}I} $. So, the current enclosed must never be zero for the magnetic field to exist. While calculating the circumference of the toroid the average of the two radii is used. During substitution, all the values involved must be expressed in their respective S.I. units. Here, $l = 51\pi {\text{cm}}$ is converted to $l = 0.51\pi {\text{m}}$ while substituting in equation (1).