Question

A triangle having vertices as $P\left( \cos \alpha ,\sin \alpha \right),Q\left( \cos \beta ,\sin \beta \right),R\left( \cos \gamma ,\sin \gamma \right)$, whose orthocentre is $\left( 0,0 \right)$. Then, the value of $\cos \left( \alpha -\beta \right)+\cos \left( \beta -\gamma \right)+\cos \left( \gamma -\alpha \right)$ is
A. $\dfrac{-3}{2}$
B. $\dfrac{-1}{2}$
C. $\dfrac{1}{2}$
D. $\dfrac{3}{2}$

Answer 1

Hint: The centroid of the triangle divides the line joining orthocentre and the circumcentre in the ratio \[2:1\].

The given vertices of the triangle are \[P(\cos \alpha ,\sin \alpha ),Q\left( \cos \beta ,\sin \beta \right)\] and \[R\left( \cos \gamma ,\sin \gamma \right)\].

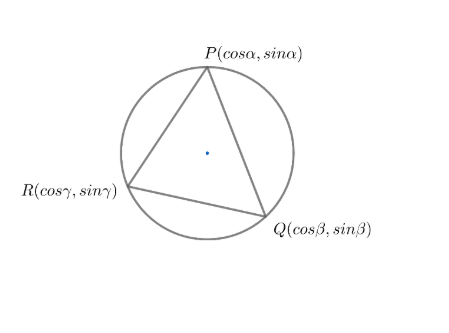
Now, we will consider the circumcircle of the triangle.
To find the equation of the circumcircle , we will see the vertices of the triangle.
By observation , we can conclude that all the vertices of the triangle satisfy the equation \[{{x}^{2}}+{{y}^{2}}=1\]
So , the equation of the circumcircle will be \[{{x}^{2}}+{{y}^{2}}=1......(i)\]
Now , we know the general equation of circle with centre at \[(a,b)\] and radius \[r\] is given as
\[{{(x-a)}^{2}}+{{(y-b)}^{2}}={{r}^{2}}\]
 Compared with equation\[(i)\], we can say that the centre of the circle represented by equation \[(i)\] is \[(0,0)\] and radius is \[1\] units.
So, the centre of the circumcircle is \[(0,0)\] and hence the circumcentre is \[(0,0)\].
Now, we know the centroid of the triangle divides the line joining orthocentre and the circumcentre in the ratio \[2:1\].
Now, in the question it is given that the orthocentre of \[\vartriangle ABC\] is \[(0,0)\] and from equation\[(i)\] we get that the circumcentre is also \[(0,0)\].
So , centroid is also \[(0,0)\].
We know , if a triangle has vertices \[\left( {{x}_{1}},{{y}_{1}} \right),\left( {{x}_{2}},{{y}_{2}} \right)\]and \[\left( {{x}_{3}},{{y}_{3}} \right)\] then , its centroid is given as
\[\left( \left( \dfrac{{{x}_{1}}+{{x}_{2}}+{{x}_{3}}}{3} \right),\left( \dfrac{{{y}_{1}}+{{y}_{2}}+{{y}_{3}}}{3} \right) \right)\]
So , \[\left( \left( \dfrac{\cos \alpha +\cos \beta +\cos \gamma }{3} \right),\left( \dfrac{\sin \alpha +\sin \beta +\sin \gamma }{3} \right) \right)=\left( 0,0 \right)\]
Now,
\[\begin{align}
  & \dfrac{\cos \alpha +\cos \beta +\cos \gamma }{3}=0 \\
 & \Rightarrow \cos \alpha +\cos \beta +\cos \gamma =0 \\
\end{align}\]
  \[\Rightarrow \cos \alpha +\cos \beta =-\cos \gamma \]
Now , we will square both sides .
On squaring on both the sides, we get
\[\Rightarrow {{\cos }^{2}}\alpha +{{\cos }^{2}}\beta +2\cos \alpha \cos \beta ={{\cos }^{2}}\gamma ......(ii)\]
Again , we have \[\dfrac{\sin \alpha +\sin \beta +\sin \gamma }{3}=0\]
\[\Rightarrow \sin \alpha +\sin \beta +\sin \gamma =0\]
\[\Rightarrow \sin \alpha +\sin \beta =-\sin \gamma \]
Now , we will square both sides .
On squaring on both the sides, we get
\[\Rightarrow {{\sin }^{2}}\alpha +{{\sin }^{2}}\beta +2\sin \alpha \sin \beta ={{\sin }^{2}}\gamma .......(iii)\]
Adding \[(ii)\]and \[(iii)\] we get ,\[\left( {{\cos }^{2}}\alpha +{{\sin }^{2}}\alpha \right)+\left( {{\cos }^{2}}\beta +{{\sin }^{2}}\beta \right)+2\left( \cos \alpha \cos \beta +\sin \alpha \sin \beta \right)=\left( {{\cos }^{2}}\gamma +{{\sin }^{2}}\gamma \right)\]
We know , \[{{\cos }^{2}}\theta +{{\sin }^{2}}\theta =1\] and \[\cos A\cos B+\sin A\sin B=\cos (A-B)\] .
So , \[\left( {{\cos }^{2}}\alpha +{{\sin }^{2}}\alpha \right)+\left( {{\cos }^{2}}\beta +{{\sin }^{2}}\beta \right)+2\left( \cos \alpha \cos \beta +\sin \alpha \sin \beta \right)=\left( {{\cos }^{2}}\gamma +{{\sin }^{2}}\gamma \right)\]can be written as \[1+1+2\left( \cos \left( \alpha -\beta \right) \right)=1\]
\[\Rightarrow 2\cos \left( \alpha -\beta \right)=-1\]
\[\Rightarrow \cos \left( \alpha -\beta \right)=\dfrac{-1}{2}........(iv)\]
Now , by symmetry we can say that
\[\cos \left( \beta -\gamma \right)=\dfrac{-1}{2}......(v)\]
And \[\cos \left( \gamma -\alpha \right)=\dfrac{-1}{2}.......(vi)\]
Adding \[(iv),(v)\]and \[(vi)\], we get
\[\begin{align}
  & \cos \left( \alpha -\beta \right)+\cos \left( \beta -\alpha \right)+\cos \left( \gamma -\alpha \right)=\left( \dfrac{-1}{2} \right)+\left( \dfrac{-1}{2} \right)+\left( \dfrac{-1}{2} \right) \\
 & \Rightarrow \cos \left( \alpha -\beta \right)+\cos \left( \beta -\alpha \right)+\cos \left( \gamma -\alpha \right)=\dfrac{-3}{2} \\
\end{align}\]
So , the value of $\cos \left( \alpha -\beta \right)+\cos \left( \beta -\gamma \right)+\cos \left( \gamma -\alpha \right)$ is equal to \[\dfrac{-3}{2}\].
Option (a) \[\dfrac{-3}{2}\] is correct answer
Note: Always remember that the centroid divides the line joining orthocentre and circumcentre in the ratio \[2:1\] and not \[1:2\]. Students often get confused and make mistakes.