Question

A triangular colourful scenery is made in a wall with sides 50 cm, 50 cm and 80 cm. A golden thread is to hang from the vertex so as to just reach the side 80 cm. How much length of golden thread is required?

Answer 1

Hint: We start solving the problem by drawing the figure to represent all the given information. We then use the facts that the shortest distance from any point to a line/line segment is the perpendicular distance from that point to the line/line segment and the altitude, median and the perpendicular bisectors from the vertex which is formed by the intersection of two equal sides in an isosceles coincide to proceed through the problem. We then use the Pythagoras theorem to calculate the required length of golden thread.

Complete step-by-step answer:
According to the problem, we are given a triangular colourful scenery made in a wall with sides 50 cm, 50 cm and 80 cm. A golden thread is to hang from the vertex so as to just reach the side 80 cm. We need to find the required length of golden thread.
Let us draw the given information to get a better view.

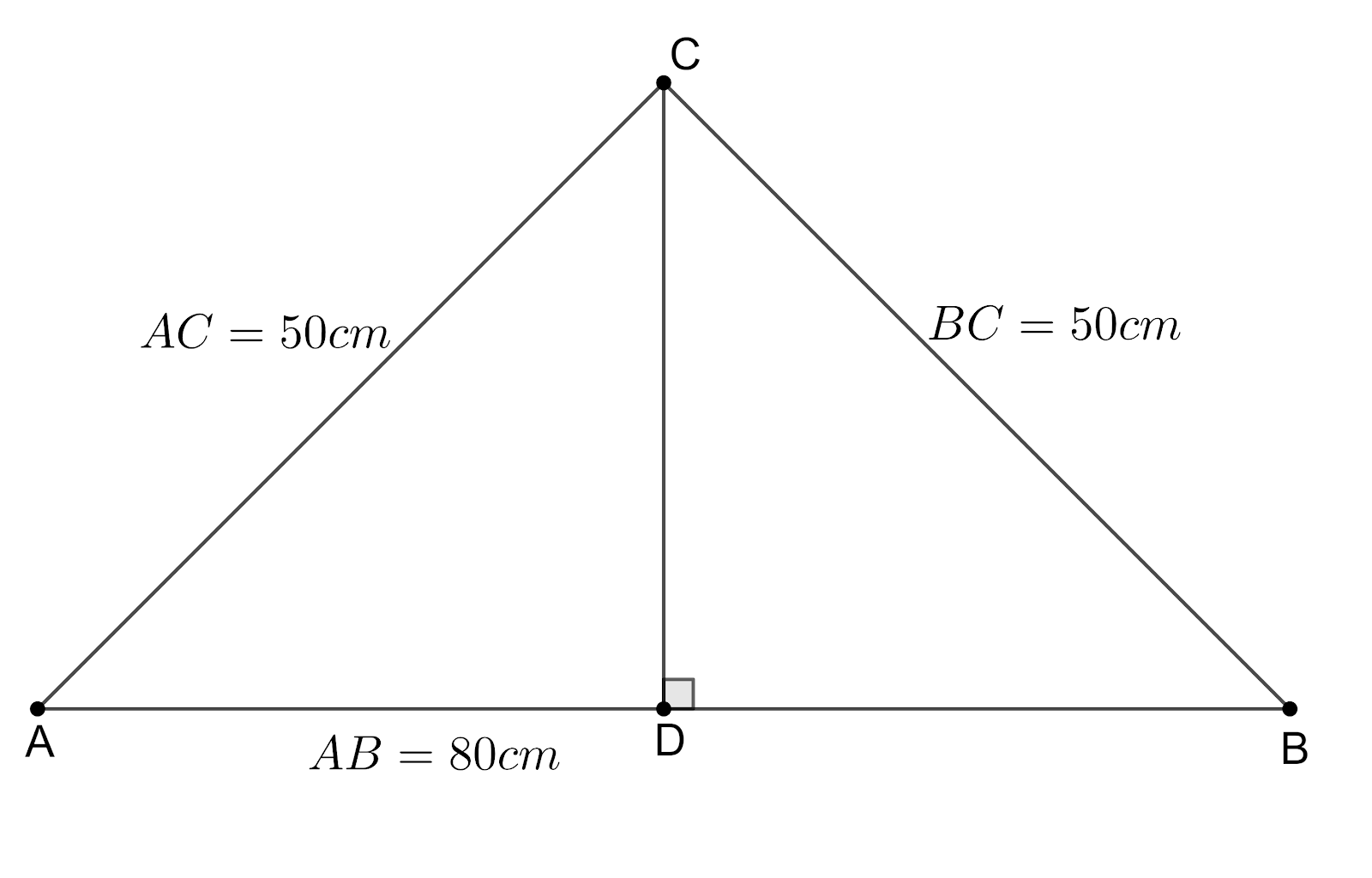
Let CD be the required length of the golden thread.
We know that the shortest distance from any point to a line/line segment is the perpendicular distance from that point to the line/line segment.
So, CD must be parallel to the side AB. We can see that the given triangle is isosceles with equal sides AC and BC. We know that the altitude, median and the perpendicular bisectors from the vertex which is formed by the intersection of two equal sides in an isosceles coincide.
We know that the median passes through the midpoint of the other side. So, point D is the midpoint of the side AB.
So, we get a length of BD = $\dfrac{1}{2}\times 80=40cm$.
From the figure, we can see that the triangle BDC is a right-angled triangle with right angle at vertex D.
We know that the sum of the squares of the other two sides of the right-angled triangle is equal to the square of the hypotenuse (from Pythagoras theorem).
So, we get $B{{C}^{2}}=B{{D}^{2}}+D{{C}^{2}}$.
$\Rightarrow {{50}^{2}}={{40}^{2}}+D{{C}^{2}}$.
$\Rightarrow 2500=1600+D{{C}^{2}}$.
$\Rightarrow D{{C}^{2}}=900$.
$\Rightarrow DC=30$.
So, we have found the required length of the golden thread as 30 cm.

Note: Whenever we get this type of problem, we first need to draw the figure representing all the given information as the diagram will itself give half of the required answer. We should not make calculation mistakes while solving this problem. We should know that the orthocentre, circumcentre and centroid lies on the line segment CD in this triangle as point C is the intersection of equal sides of the triangle.