Question

A triangular pyramid has …..faces, ……edges and …..vertices.

Answer 1

Hint: In the given question, we are supposed to find the number of faces, edges, and vertices of a triangular pyramid. We will be solving the given question using the diagram of the triangular pyramid to determine its faces, vertices, and edges.

Complete step by step solution:
We are asked to find the number of faces, vertices, and edges in a triangular pyramid. We will be solving the given question using the concept of geometry.
A pyramid is a geometrical figure that has a base and three or more triangular surfaces which meet at the apex of the pyramid.
The triangular pyramid is formed from the triangles. A triangular pyramid has a triangular base. It is also known as a tetrahedron.
The diagram of the triangular pyramid is given as follows,

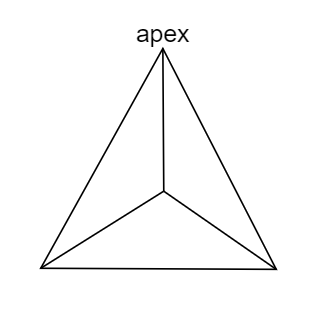
The faces, vertices, and edges are the three characteristics of the three-dimensional geometric figure.
The face is the individual flat surface of a geometric figure. It forms the part of a boundary of a geometric figure.
From the above diagram,
We can see that the triangular pyramid has four individual flat surfaces. So, the triangular pyramid has 4 faces.
An edge is a line where two faces meet. It is a line segment that acts as an interface between two faces. It is formed by joining two vertices of a geometric figure.
From the above diagram,
We can see that the triangular pyramid has 6 edges. So, the triangular pyramid has 6 edges.
A vertex is a point of intersection of two or more edges. The vertices in a geometric figure are also referred to as corners.
From the above diagram,
We can see that the triangular pyramid has 4 vertices. So, the triangular pyramid has 4 vertices.
$\therefore$ A triangular pyramid has 4 faces, 6 edges, and 4 vertices.

Note: The given question can be solved alternatively as follows,
From geometry, we know that an n-sided base has n+1 faces, 2n edges, and n+1 vertices. In the case of a triangular pyramid, we know that it has a triangular base.
From the above, we can say that the base of a triangular base is 3-sided.
Substituting the value of n = 3, we get,
$\Rightarrow faces=n+1=3+1=4$
$\Rightarrow edges=2n=2\times 3=6$
$\Rightarrow vertices=n+1=3+1=4$