
A T.V transmitting antenna is 128m tall. If the receiving is at ground level, the maximum distance between them for satisfactory communication in L.O.S mode is:
(Radius of earth=
Answer
506.4k+ views
1 likes
Hint: As per the basics of communication, the maximum distance (d) for satisfactory transmission between two antennas, with one at height (h) and the other at ground level is
Here r stands for the radius of earth.
Step by step solution:
Given in the problem, we have an antenna of perpendicular height of 128m, that is (h=128m). This antenna is on the surface of earth. The earth’s radius is given to be 6400km, that is (R=
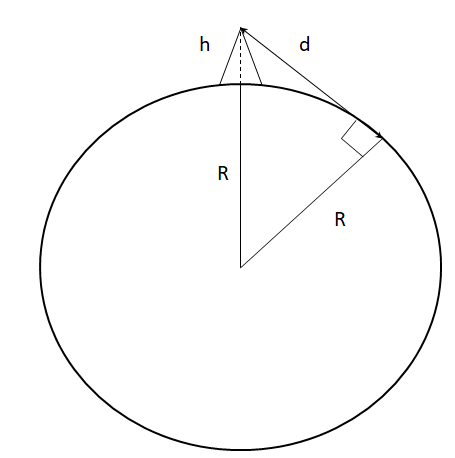
The maximum distance from the antenna at height (h) to the ground based antenna at distance (d) is given by the formula
However, since, the value of
Therefore, substituting in the values of r=
Hence, the maximum distance between the antenna at the height and the one at the ground level for satisfactory communication is
Note:
It is important to remember that L.O.S which stands for line of sight is the kind of communication over here. Hence, in this kind of communication a direct straight line based communication happens and if any obstacle obstructs or comes in between the two antennas, the communication won’t occur.
For the case when there are obstacles between two antennas, then reflection of communication signals is used which requires additional antennas in between to reflect and change the direction of signals to relay the information.
Here r stands for the radius of earth.
Step by step solution:
Given in the problem, we have an antenna of perpendicular height of 128m, that is (h=128m). This antenna is on the surface of earth. The earth’s radius is given to be 6400km, that is (R=

The maximum distance from the antenna at height (h) to the ground based antenna at distance (d) is given by the formula
However, since, the value of
Therefore, substituting in the values of r=
Hence, the maximum distance between the antenna at the height and the one at the ground level for satisfactory communication is
Note:
It is important to remember that L.O.S which stands for line of sight is the kind of communication over here. Hence, in this kind of communication a direct straight line based communication happens and if any obstacle obstructs or comes in between the two antennas, the communication won’t occur.
For the case when there are obstacles between two antennas, then reflection of communication signals is used which requires additional antennas in between to reflect and change the direction of signals to relay the information.
Latest Vedantu courses for you
Grade 10 | CBSE | SCHOOL | English
Vedantu 10 CBSE Pro Course - (2025-26)
School Full course for CBSE students
₹37,300 per year
Recently Updated Pages
Master Class 4 Maths: Engaging Questions & Answers for Success

Master Class 4 English: Engaging Questions & Answers for Success

Master Class 4 Science: Engaging Questions & Answers for Success

Class 4 Question and Answer - Your Ultimate Solutions Guide

Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Trending doubts
Give 10 examples of unisexual and bisexual flowers

Draw a labelled sketch of the human eye class 12 physics CBSE

a Tabulate the differences in the characteristics of class 12 chemistry CBSE

Differentiate between homogeneous and heterogeneous class 12 chemistry CBSE

Why is the cell called the structural and functional class 12 biology CBSE

Differentiate between insitu conservation and exsitu class 12 biology CBSE




