Question

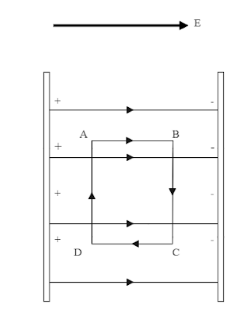
A uniform electric field exists between two charged plates as shown in the figure. What should be the work done in moving a charge q along the closed rectangular path ABCDA.

Answer 1

Hint: Work done is a property that depends on displacement of the object the force is subjected on. $workdone=force\times displacement$ . We need to find the displacement the charge travels through the loop ABCDA.

Formula Used: We will be using the notion that force is conservative and work done by an electric charge $q$ in an uniform electric field $E$ is given by $w=Ed\cos \theta$ where $w$ is the work done by the charge, $d$ is the displacement due to the force applied on the charge (which in this case is an electrostatic force), and $\theta$ is the angle between the two vectors.

Complete Step by Step solution
We know, in a uniform electric field the field lines are going to move from positively charged plate to the negatively charged one. Now suppose you are placing a charge in between the plates like shown in the figure below. Also consider an imaginary rectangular path ABCD with dimensions, $AB=d_1=CD$ and $BC=d_2=DA$ .

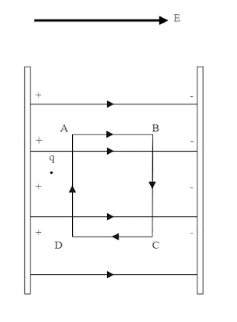
Now let us consider the work done to move the charge from point A to B between the plates.
 $w=E{d}_1\cos 0^{\circ }$
Here $\theta =0^{\circ }$ , because the work done on the point to move from A to B and the electric field lines are in the same direction.
We also know that, $\cos 0^{\circ }=1$ . So, $w=E{d}_1(1)$
 $w=E{d}_1$
Similarly, along the path $BC=d_2$ , the angle between the two vectors is, $\theta ={90}^{\circ }$ . $w=E{d}_2\cos {90}^{\circ }$
 $w=E{d}_2(0)$
And thus, the work done to move charge on the path BC,
 $w=0J$
Similarly for path CD we can see that the angle between the vectors $\theta$ is ${180}^{\circ }$ . We know that $\cos {180}^{\circ }=-1$ . Thus, making work done along the path CD, $w=E{d}_1\cos {180}^{\circ }$ .
 $w=E{d}_1(-1)$
 $w=-E{d}_1$
Also, for the path DA, the angle $\theta$ is ${270}^{\circ }$ . Thus, the work done can be given by $w=E{d}_2\cos {270}^{\circ }$ . Now we can find the work done along the path DA as $w=E{d}_2(0)$ . Since, $\cos {270}^{\circ }=0$ .
 $w=0$
Now that we have the work done to move the charge $q$ along the closed path ABCDA. Let us calculate the total work done by adding the work done to move the charge along each side.
 $w=E{d}_1+0+(-E{d}_1)+0$
 $w=0$
Thus, the work done is zero. No actual work is done to move a charge around the closed path ABCDA as shown in the figure.

Note
Alternate solution-
Since we can see that the charge is supposed to travel along the path ABCDA. The particle starts from A and ends up back in A, thus making the displacement $d=0$ . Work is a quantity whose magnitude depends on the displacement, thus the work done is
 $w=Ed\cos \theta$
 $w=E(0)\cos \theta$
Thus, making the work done zero. This simple logic can be used to solve the problem faster.