Question

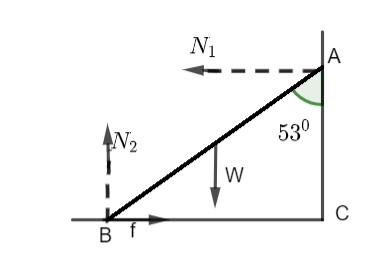
A uniform ladder of mass $10\,kg$ leans against a smooth vertical wall making an angle of ${53^0}$ with it. The other end rests on a rough horizontal surface. Find the normal force and the friction force that the floor exerts on the ladder.

Answer 1

Hint: Since the ladder is in equilibrium, the sum of all the forces and torques acting on the ladder must be zero. So, $\sum {{F_x} = 0} $ , $\sum {{F_y} = 0} $ and ${\tau _{net}} = 0$ . We shall equate the forces in the vertical and horizontal directions. After that we shall equate the net torque acting about point A to zero. The torque will be due to forces W and ${N_1}$ only since these forces do not pass through point A.
Then we will express the distances BC and AC in terms of the components of AB in the x and y directions. Making proper substitutions, we will get all the forces.

Complete step by step solution:
To maintain the vertical equilibrium, $\sum {{F_y} = 0} $ .This means that ${N_2} = W$ .
Now $W = mg$ which is the weight of the rod. The mass is given to be $10\,kg$ .
Substituting the known values we get,
$W = 10 \times 9.8$
$ \Rightarrow W = 98\,N$
Hence, ${N_2} = W = 98\,N$
To maintain the horizontal equilibrium, $\sum {{F_x} = 0} $ . This means that ${N_1} = f$
Now torque about a point acting due to a force is given as the cross product of the force acting and the distance of the point from the contact point where the force is acting.
Mathematically it is given as $\tau = Fr\sin \theta $ where F is the force applied, r is the distance and $\theta $ is the angle between the vectors.
About point A,
To maintain equilibrium, ${\tau _{net}} = 0$ .
Let’s draw the projection of the point where W acts to the surface and name it as D.

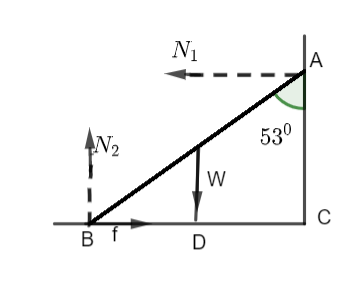
Now we have to equate the torques acting due to W and ${N_1}$ to zero. Hence,
 ${N_1} \times AC = W \times BD$
Now if we redraw the triangle, we have,

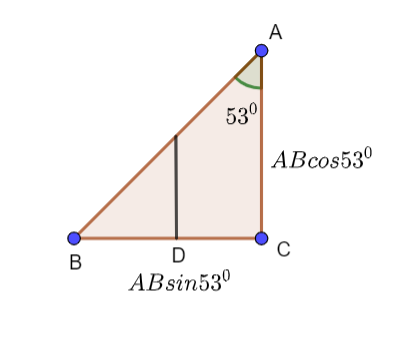
So, using the components of AB in x and y directions we have
$AC = AB\cos {53^0}$ and $BC = AB\sin {53^0}$
Also, $BD = \dfrac{{BC}}{2}$ , we can say that $BD = \dfrac{{AB\sin {{53}^0}}}{2}$
Substituting the required values in the torque equation, we get,
${N_1} \times AB\cos {53^0} = W \times \dfrac{{AB\sin {{53}^0}}}{2}$
Simplifying the expression we have,
${N_1}\cos {53^0} = \dfrac{{W\sin {{53}^0}}}{2}$
Now we know that $\cos {53^0} = \dfrac{3}{5}$ and $\sin {53^0} = \dfrac{4}{5}$ .
Also, we calculated that $W = 98\,N$
Substituting the values, we get,
${N_1} \times \dfrac{3}{5} = \dfrac{{98}}{2} \times \dfrac{4}{5}$
Further solving this equation, we get,
${N_1} = \dfrac{{98 \times 2}}{3}$
$ \Rightarrow {N_1} = 65.3\,N$
We also calculated before that ${N_1} = f$
Hence, ${N_1} = f = 65.3\,N$ and ${N_2} = W = 98\,N$.

Note: We do not take into consideration those forces which directly pass from the point for which we are writing the torque equation because the distance would be zero and hence the torque would be zero. So, there is no point in including these forces. Also, since a rod is a rigid body, it will have the tendency to rotate about a point or axis. Hence to maintain equilibrium, it is necessary to conserve torque for such bodies.