Question

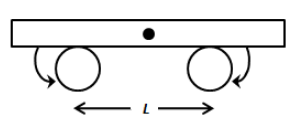
A uniform plate of mass M stays horizontally and symmetrically on two wheels rotating in opposite directions as shown in figure. The separation between the wheels is L. The friction coefficient between each wheel and the plate is \[\mu \] . Find the time period of oscillation of the plate if it is slightly displaced along its length and released.

Answer 1

Hint:Use the law of conservation of torque and determine the frictional force between the wheel and plate for each wheel. The restoring force for the oscillation is due to the net frictional force. Recall the acceleration of the particle in simple harmonic motion and determine the angular frequency.

Formula used:
Torque, \[\tau = rF\] ,
where, F is the force and r is the distance from the point of action of force and origin.
Time period, \[T = \dfrac{{2\pi }}{\omega }\] ,
where, \[\omega \] is the angular frequency.

Complete step by step answer:
Let the plate be displaced towards the left by distance x, therefore, the centre of gravity of the plate also moves by distance x.

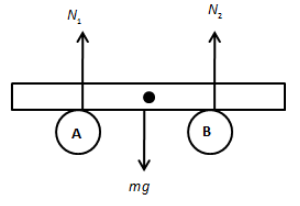
In the equilibrium position, we can write,
 \[{N_1} + {N_2} = mg\] …… (1)
Now, let us take the moment about the centre of gravity of the plate as follows,
 \[{N_2}\left( {\dfrac{L}{2} + x} \right) = {N_1}\left( {\dfrac{L}{2} - x} \right)\]
Using equation (1) in the above equation, we can write,
 \[\left( {mg - {N_1}} \right)\left( {\dfrac{L}{2} + x} \right) = {N_1}\left( {\dfrac{L}{2} - x} \right)\]
 \[ \Rightarrow \left( {mg\dfrac{L}{2} - {N_1}\dfrac{L}{2} + mgx - {N_1}x} \right) = {N_1}\dfrac{L}{2} - {N_1}x\]
 \[ \Rightarrow {N_1}\dfrac{L}{2} + {N_1}\dfrac{L}{2} = mg\left( {x + \dfrac{L}{2}} \right)\]
 \[ \Rightarrow {N_1}L = mg\left( {\dfrac{{2x + L}}{2}} \right)\]
 \[ \Rightarrow {N_1} = \dfrac{{mg\left( {L + 2x} \right)}}{{2L}}\] …… (2)

Similarly, we can write,
 \[{N_2} = \dfrac{{mg\left( {L - 2x} \right)}}{{2L}}\] …… (3)
The frictional force acting on the plate due to each wheel is,
 \[{f_1} = \mu {N_1} = \dfrac{{\mu mg\left( {L + 2x} \right)}}{{2L}}\] …… (4)
And,
 \[{f_2} = \mu {N_2} = \dfrac{{\mu mg\left( {L - 2x} \right)}}{{2L}}\] …… (5)
We can express the restoring force as,
 \[F = {f_1} - {f_2}\]
 \[ \Rightarrow F = \dfrac{{\mu mg\left( {L + 2x} \right)}}{{2L}} - \dfrac{{\mu mg\left( {L - 2x} \right)}}{{2L}}\]
 \[ \Rightarrow F = \dfrac{{\mu mg}}{{2L}}\left( {4x} \right)\]
 \[ \Rightarrow F = \dfrac{{2\mu mg}}{L}x\]

We have the acceleration produced in the plate is,
 \[a = \dfrac{F}{m} = \dfrac{{\dfrac{{2\mu mg}}{L}x}}{m}\]
 \[ \Rightarrow a = \dfrac{{2\mu g}}{L}x\] …… (6)
But, we have the acceleration of the plate is,
 \[a = {\omega ^2}x\]
 \[ \Rightarrow {\omega ^2} = \dfrac{a}{x}\]
Using equation (6) in the above equation, we get,
 \[{\omega ^2} = \dfrac{{\dfrac{{2\mu g}}{L}x}}{x}\]
 \[ \Rightarrow {\omega ^2} = \dfrac{{2\mu g}}{L}\]
 \[ \Rightarrow \omega = \sqrt {\dfrac{{2\mu g}}{L}} \]
We have the expression for the time period of the oscillation,
 \[T = \dfrac{{2\pi }}{\omega }\]
 \[ \therefore T = 2\pi \sqrt {\dfrac{L}{{2\mu g}}} \]

This is the expression for the time period of the oscillation of the plate.

Note:The moment about the centre of gravity is the conservation of torque. The torque due to wheel A and torque due to wheel B is the same and that is why we write \[{N_2}\left( {\dfrac{L}{2} + x} \right) = {N_1}\left( {\dfrac{L}{2} - x} \right)\] . Students often write the acceleration as \[a = \omega x\] . But the acceleration of the particle performing SHM is proportional to square of the angular frequency, that is \[a = {\omega ^2}x\] .