Question

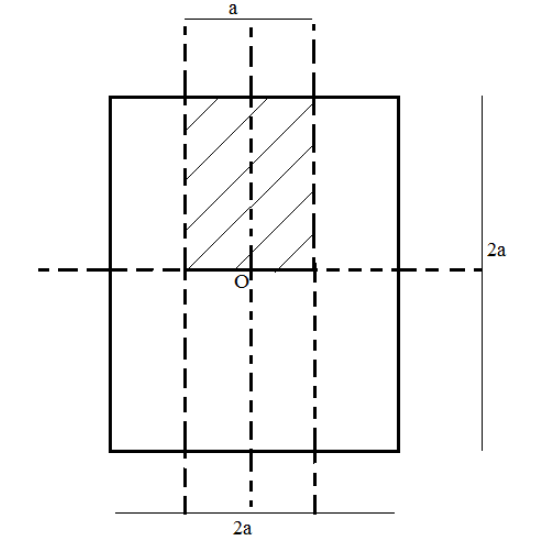
A uniform sheet is shown below. If the shaded area is removed, find the new position of the centre of mass?

A. \[ + \dfrac{a}{6}\]
B. \[ - \dfrac{a}{6}\]
C. \[ + \dfrac{a}{3}\]
D. \[ - \dfrac{a}{3}\]

Answer 1

Hint:The new position of the centre of mass = [The centre of mass of the entire sheet]-[The centre of mass of the shaded area].Find the above two centre of masses using the law of symmetry

Complete step by step answer:
Let the centre of mass be represented as COM and the new position of the centre of mass be R. Thus, R= COM (entire sheet) – COM (shaded area)
According to the law of symmetry, the centre of mass of a symmetric object with uniform density lies at its geometric centre.Thus COM (entire sheet) lies at the origin (0,0) and the COM(shaded area) lies at $\left( {0,\dfrac{a}{2}} \right)$.
Let the mass of the entire sheet be M,
Now, the area of the entire sheet is
\[A = 2a \times 2a = 4{a^2}\]
The area of the shaded area is
\[A' = a \times a = {a^2}\]
Here, the area of the shaded region is 4 times lesser than the entire sheet, so 4 such areas are needed to build the entire sheet, hence the mass of the shaded area M/4.

Mass of remaining sheet is \[M - \dfrac{M}{4} = \dfrac{{3M}}{4}\]
New position of COM will be;
\[
R = \dfrac{{M(0,0) - \dfrac{M}{4}(0,\dfrac{a}{2})}}{{\dfrac{{3M}}{4}}} \\
\Rightarrow R = \dfrac{{ - \dfrac{{Ma}}{8}}}{{\dfrac{{3M}}{4}}} \\
\therefore R = \dfrac{{ - a}}{6} \\
\]

>Hence, option B is the correct answer.

Note:Students must note the law of symmetry in the case of the centre of mass, where the centre of mass lies at its geometric centre. Here, the mass is taken out from the upper region of the origin, thus, the mass density of sheet in the lower region would be more than that of the upper region. Hence the centre of mass would shift below the origin, giving us a negative value of the Y-axis. Hence, we can eliminate two of the options straight, and can also cross-check our answer through this.