Question

A vertical pole stands at a point O on a horizontal ground. A and B are points on the ground d meters apart. The pole subtends angles \[\alpha \] and \[\beta \] at A and B respectively. AB subtends an angle \[\gamma \] at O, the height of the pole is

Answer 1

Hint:
The formula for writing tangent of an angle is
\[\tan \theta =\dfrac{perpendicular}{base}\] .
Another important formula that may be used in the question is the cosine rule which is
\[{{b}^{2}}={{a}^{2}}+{{c}^{2}}-2ac\cos B\]
(Where a, b and c are the side lengths of the triangle and B is the angle opposite to the side length b)

Complete step by step answer:
As mentioned in the question, the figure would look like the below picture

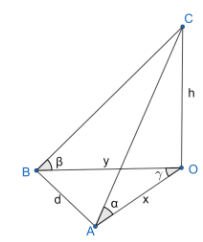
(Where the height of the vertical pole is taken to be as ‘h’)
Let the distance between A and O be x and the distance between B and O be y.
Now, firstly using the tangent formula in triangle with \[\alpha \] angle as follows
\[\begin{align}
  & \tan \alpha =\dfrac{h}{x} \\
 & x=h\cot \alpha \ \ \ \ \ ...(1) \\
\end{align}\]
Secondly, using the tangent formula again in the triangle with \[\beta \] angle as follows
\[\begin{align}
  & \tan \beta =\dfrac{h}{y} \\
 & y=h\cot \beta \ \ \ \ \ ...(2) \\
\end{align}\]
Now, using the cosine formula in the \[\vartriangle AOB\]as follows
 \[{{d}^{2}}={{x}^{2}}+{{y}^{2}}-2xy\cos \gamma \ \ \ \ \ ...(a)\]
Now, putting equations (1) and (2) in equation (a) as follows, we get
\[\begin{align}
  & {{d}^{2}}={{h}^{2}}{{\cot }^{2}}\alpha +{{h}^{2}}{{\cot }^{2}}\beta -2(h\cot \alpha )(h\cot \beta )\cos \gamma \\
 & {{d}^{2}}={{h}^{2}}{{\cot }^{2}}\alpha +{{h}^{2}}{{\cot }^{2}}\beta -2{{h}^{2}}\cdot \cot \alpha \cdot \cot \beta \cdot \cos \gamma \\
 & {{d}^{2}}={{h}^{2}}\left( {{\cot }^{2}}\alpha +{{\cot }^{2}}\beta -2\cot \alpha \cdot \cot \beta \cdot \cos \gamma \right) \\
 & {{h}^{2}}=\dfrac{{{d}^{2}}}{\left( {{\cot }^{2}}\alpha +{{\cot }^{2}}\beta -2\cot \alpha \cdot \cot \beta \cdot \cos \gamma \right)} \\
\end{align}\]
Now, on taking square root on both the sides, we get the height of the vertical pole that is standing on point O is
\[h=\dfrac{d}{{{\left( {{\cot }^{2}}\alpha +{{\cot }^{2}}\beta -2\cot \alpha \cdot \cot \beta \cdot \cos \gamma \right)}^{\dfrac{1}{2}}}}\]

Note:
The figure in this question is very tricky and is difficult to visualize it at first. Hence, the students can make an error while drawing the figure and then end up making a mistake and they would get to the correct solution. We can also solve the sides of the triangle using sine rule and then convert into cosine form.