Question

A vertical tower stands on a horizontal plane and is surrounded by a vertical flagstaff of height h meter. At a point on the plane. The angle of elevation of the bottom of the flag staff is $\alpha $and that of the top is $\beta $. Prove that the height of the tower is $\dfrac{h\tan \alpha }{\tan \beta -\tan \alpha }$.

Answer 1

Hint: Draw the figure assuming tower and flag staff as straight. You will find 2 triangles. Take the elevations as given in the question. By using the definition of tangent of angles. Find the tan of both elevations in terms of height of tower and height of flagstaff. By using the condition that the horizontal distance is the same equate the terms you get for horizontal distance in both equations. You will get the height of flagstaff in terms of height of tower and angle of elevations.

Complete step-by-step answer:
Tangent of angle: -
Tangent of angle a triangle is defined as the ratio of side opposite to the angle to the side length which is adjacent to the angle.
Let us take angle n in triangle ABC. Then $\text{tan }x$ is

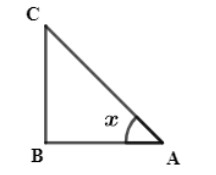
$\text{tan }x\ =\ \dfrac{\text{BC}}{\text{AB}}$
Draw the diagram with height of y and height of flag staff is h. Angle of elevations being $\alpha ,\ \beta $. The figure described above is as shown below.

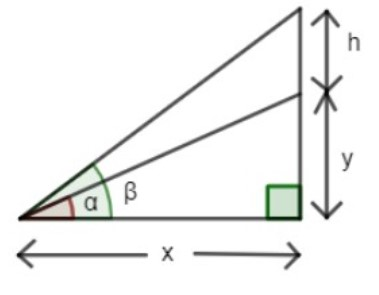
By applying tangent on the elevations of the tower; $\alpha $ we get:
\[\text{tan }\alpha \ =\ \dfrac{y}{x}\]
By cross multiplication of terms, we get: \[x\ =\ \dfrac{y}{\text{tan }\alpha }\] ……………………(i)
By applying tangent on the elevation of (tower $+$flag); $\beta $, we get:
 \[\text{tan }\beta \ =\ \dfrac{h+y}{x}\]
By cross multiplication of terms in above equation we get:
 \[x\ =\ \dfrac{h+y}{\text{tan }\beta }\]…………………………………………………(ii)
By equating the equation (i) and equation (ii), we get:
$\dfrac{y}{\tan \alpha }\ =\ \dfrac{h+y}{\tan \beta }$
By cross multiplication of terms in equation above, we get:
$y\tan \beta \ =\ h\tan \alpha +y\tan \alpha $
By, simplifying the above equation, we get finally:
$y\ =\ \dfrac{h\tan \alpha }{\tan \beta -\tan \alpha }$
Hence, proved the required equation in the given question.

Note: While applying tan to the elevation of the top of the flag don’t forget to consider the height of the tower also as $\beta $ includes that. Now the height for the elevation $\beta $ becomes h + y. Be careful while applying tan of angle take the whole length of opposite side in numerator and then length of adjacent side. Generally students tend to confuse the terms x, y. y is vertical height and x is horizontal distance.