Question

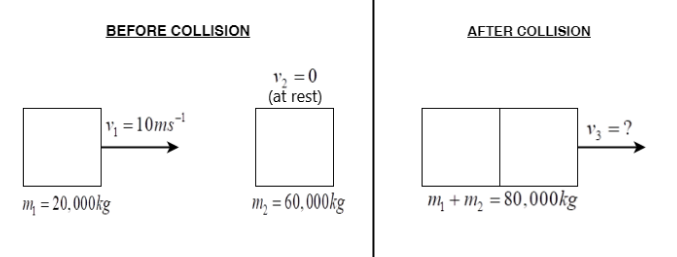
A wagon of 20 metric ton moves with $10m{s^{ - 1}}$ and collides perfectly inelastically with a stationary wagon of 60 metric ton. Find loss of kinetic energy.
A. 250 KJ
B. 750 KJ
C. 500 KJ
D. 650 KJ

Answer 1

Hint: It is given that the collision is inelastic, which means that after collision the two wagons will move together with a same velocity, for finding the final velocity of the two wagons apply the principle of conservation of linear momentum that is – momentum before collision = momentum after collision.After finding the final velocity, find the initial and final kinetic energies of the system, where kinetic energy is given by $\dfrac{1}{2}m{v^2}$ . Finding the difference between the initial and final kinetic energies, we will get the loss of kinetic energy that is the required answer.

Complete step by step solution:
Let the mass of the two wagons be ${m_1}$ and ${m_2}$ respectively.And let the velocity of the wagons before collision be ${v_1}$ and ${v_2}$ .We are given that:
Mass of the wagons is:
$
{m_1} = 20ton = 20 \times 1000kg = 20,000kg\,\,\,(\because 1ton = 1000kg) \\
\Rightarrow{m_2} = 60ton = 60,000kg \\ $
And velocity of wagons before collision:
$
{v_1} = 10m{s^{ - 1}} \\
\Rightarrow{v_2} = 0{\text{ }}\left( {{\text{at rest}}} \right) \\ $
Let the final velocity of the coupled wagons after collision be ${v_3}$ .

Now, applying the principle of conservation of linear momentum for finding the final velocity of the wagons, we get –
momentum before collision = momentum after collision
$
\Rightarrow {m_1}{v_1} + {m_2}{v_2} = \left( {{m_1} + {m_2}} \right){v_3} \\
\Rightarrow 20,000 \times 10 + 60,000 \times 0 = \left( {20,000 + 60,000} \right) \times {v_3} \\
\Rightarrow 2 \times {10^5} = 8 \times {10^4} \times {v_3} \\
\Rightarrow {v_3} = \dfrac{{2 \times {{10}^5}}}{{8 \times {{10}^4}}} \\
\Rightarrow {v_3} = \dfrac{{20}}{8} \\
\Rightarrow {v_3} = 2.5{\text{ m}}{{\text{s}}^{ - 1}} \\ $
So, the final velocity of the wagons is $2.5m{s^{ - 1}}$ .Now, finding the change in kinetic energy of the system:
Change in kinetic energy = final kinetic energy – initial kinetic energy
\[
\Delta K.E = K.{E_f} - K.{E_i} \\
\Rightarrow\Delta K.E = \dfrac{1}{2}\left( {{m_1} + {m_2}} \right)v_3^2 - \left( {\dfrac{1}{2}{m_1}v_1^2 + \dfrac{1}{2}{m_2}v_2^2} \right) \\
\Rightarrow\Delta K.E = \dfrac{1}{2} \times 8 \times {10^4} \times {\left( {\dfrac{5}{2}} \right)^2} - \left( {\dfrac{1}{2} \times 2 \times {{10}^4} \times {{10}^2} + \dfrac{1}{2} \times 6 \times {{10}^4} \times 0} \right) \\
\Rightarrow\Delta K.E = \dfrac{1}{2} \times 8 \times {10^4} \times \dfrac{{25}}{4} - \left( {{{10}^6} + 0} \right) \\
\Rightarrow\Delta K.E = 0.25 \times {10^6} - {10^6} \\
\Rightarrow\Delta K.E = - 0.75 \times {10^6}J \\
\therefore\Delta K.E = - 750 \times {10^3}J = - 750{\text{ }}kJ \\
\]
Here, the negative sign shows that there is loss of kinetic energy. Loss of kinetic energy = 750 kJ.

Hence, option B is correct.

Note: It is given that the collision is inelastic, it means that after the collision both the wagons will be stuck together and they will move with the same velocity being coupled. One should remember that there is always loss of kinetic energy in a perfectly inelastic collision, while there is no loss of kinetic energy in a perfectly elastic collision.