Question

A wire of length 28m is to be cut into two pieces. One of the pieces is to be made into a square and the other into a circle. What should be the length of the two pieces so that the combined area of the square and the circle is minimum?

Answer 1

Hint: Put the length of the first part as ‘x’ and 2nd part as (28 - x). Take x as the perimeter of the square and (28 - x) as the perimeter of the circle. Find the side of the square and radius of the square. Then find the combined length of square and radius such that their area is minimum.

Complete step-by-step answer:
It’s said that a wire of 28m length is cut into 2 parts. We don’t know the length at which it was cut. So, let us consider the length of the first part as ‘x’.
So, the length of the second part will be (28 - x), as 28m is the total length of wire.
It’s said that one part of the wire is converted into a square and the other part is converted into a circle.
Let us consider that the length x m is converted into a square.

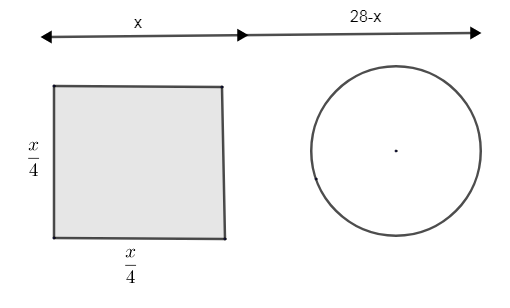
We know a square has 4 sides. Thus the perimeter of the square is the sum of the length of its side. As the length of sides of a square is the same, we can make out that \[4\times \](side of square) is equal to the length x.
i.e. x is the perimeter of the square, as the wire is converted into the shape of a square.
\[\therefore \] \[4\times \](side of square) = x.
\[\therefore \] One side of the square\[=\dfrac{x}{4}\]
\[\therefore \] Side of square\[=\dfrac{x}{4}-(1)\]
The length (28 - x) m is converted into a circle. Let ‘r’ be the radius of the circle formed.
As the wire is converted into a shape of the circle, the circumference of the circle becomes equal to (28 - x) m.
 \[\therefore \] Circumference = 28 – x.
We know the circumference of a circle with radius r =\[2\pi r\].
\[\begin{align}
  & \therefore 2\pi r=28-x \\
 & \therefore r=\left( \dfrac{28-x}{2\pi } \right)m-(2) \\
\end{align}\]
What we need to find is the combined length of pieces so that the combined area of circle and square is minimum.
Now let us consider the total area of the circle and square as T.
\[\therefore \] T = area of circle + area of square.
We know the area of the circle \[=\pi {{r}^{2}}\], with radius r.
Area of square \[={{\left( side \right)}^{2}}\]
\[\therefore T=\pi {{r}^{2}}+{{\left( side \right)}^{2}}-(3)\]
Substitute the value of r from equation (2) and side of square from equation (1) in equation (3) we get,
\[T=\pi {{\left( \dfrac{28-x}{2\pi } \right)}^{2}}+{{\left( \dfrac{x}{4} \right)}^{2}}-(4)\]
Now let us differentiate T with respect to x.
\[\dfrac{dT}{dx}=\dfrac{d}{dx}\left[ \dfrac{\pi }{4{{\pi }^{2}}}\times {{\left( 28-x \right)}^{2}} \right]+\dfrac{d}{dx}\left( \dfrac{{{x}^{2}}}{16} \right)\]
\[=\dfrac{1}{4\pi }\left[ 2\left( 28-x \right)\times \dfrac{d}{dx}\left( 28-x \right) \right]+\dfrac{2x}{16}\]
\[\dfrac{dT}{dx}=\left( \dfrac{28-x}{2\pi } \right)\left( -1 \right)+\dfrac{x}{8}-(5)\]
Put, \[\dfrac{dT}{dx}=0\]
\[\begin{align}
  & \therefore \left( \dfrac{28-x}{2\pi } \right)\left( -1 \right)+\dfrac{x}{8}=0 \\
 & \therefore \dfrac{x}{8}=\dfrac{28-x}{2\pi } \\
\end{align}\]
Cross multiplying the above equation,
\[\begin{align}
  & 2\pi x=8\left( 28-x \right) \\
 & 2\pi x=224-8x \\
 & \Rightarrow 2\pi x+8x=224 \\
\end{align}\]
Now simplify the expression by dividing it by 2.
\[\begin{align}
  & 2\pi x=8\left( 28-x \right) \\
 & \pi x+4x=112 \\
 & \Rightarrow x\left( \pi +4 \right)=112 \\
 & x=\dfrac{112}{4+\pi }-(6) \\
\end{align}\]
Now let us find, \[\dfrac{{{d}^{2}}T}{d{{x}^{2}}}=\dfrac{d}{dx}\left[ \dfrac{-28+x}{2\pi }+\dfrac{x}{8} \right]\]
\[\begin{align}
  & =\dfrac{1}{2\pi }\dfrac{d}{dx}\left( -28+x \right)+\dfrac{1}{8}\dfrac{d}{dx}x \\
 & =\dfrac{1}{2\pi }\times 1+\dfrac{1}{8}\times 1=\dfrac{1}{2\pi }+\dfrac{1}{8} \\
\end{align}\]
\[\therefore \dfrac{{{d}^{2}}T}{d{{x}^{2}}}=\dfrac{1}{2\pi }+\dfrac{1}{8}\], which is greater than zero.
Hence, \[\dfrac{{{d}^{2}}T}{d{{x}^{2}}}>0\] at \[x=\dfrac{112}{4+\pi }\]. Hence, we can say that at \[x=\dfrac{112}{4+\pi }\] total area is minimum.
Now let us find the length of the other part.
Length of other part =28 – x
\[=28-\dfrac{112}{4+\pi }=\dfrac{28\left( 4+\pi \right)-112}{\left( 4+\pi \right)}\]
Simplify the expression,
\[\begin{align}
  & =\dfrac{112+28\pi -112}{4+\pi } \\
 & =\dfrac{28\pi }{4+\pi } \\
\end{align}\]
\[\therefore \]Length of 1st part\[=\dfrac{112}{4+\pi }\]
Length of 2nd part\[=\dfrac{28\pi }{4+\pi }\]

Note:
Now let us consider the first part of length ‘x’ as circumference of circle and (28 - x) as the perimeter of the square.
The radius of circle, \[2\pi r=x\Rightarrow r=\dfrac{x}{2\pi }\]
Side of the square\[=\dfrac{side}{4}=\dfrac{28-x}{4}\]
Total area, \[T={{\left( \dfrac{28-x}{4} \right)}^{2}}+{{\left( \dfrac{x}{2\pi } \right)}^{2}}\times \pi \]
Differentiate T w.r.t to x.
\[\begin{align}
  & \dfrac{dT}{dx}=\dfrac{1}{16}\times 2\left( 28-x \right)\left( -1 \right)+\dfrac{\pi }{4{{\pi }^{2}}}\times 2x \\
 & =\dfrac{-\left( 28-x \right)}{8}+\dfrac{x}{2\pi } \\
\end{align}\]
Put, \[\dfrac{dT}{dx}=0\]
\[\Rightarrow \dfrac{28-x}{8}=\dfrac{x}{2\pi }\]
Cross multiplying and solving, we get,
\[\begin{align}
  & 2\pi \left( 28-x \right)=8x \\
 & 56\pi -2\pi x=8x \\
 & \Rightarrow 28\pi -\pi x=4x \\
 & \Rightarrow x\left( 4+\pi \right)=28\pi \\
 & \therefore x=\dfrac{28\pi }{4+\pi } \\
\end{align}\]
Taking, \[\dfrac{{{d}^{2}}T}{d{{x}^{2}}}=\dfrac{d}{dx}\left( \dfrac{x-28}{8}+\dfrac{x}{2\pi } \right)=\dfrac{1}{8}+\dfrac{1}{2\pi }>0\]
Length of 1st part, \[x=\dfrac{28\pi }{4+\pi }\]
Length of 2nd part, \[x=28-x=28-\dfrac{28\pi }{4+\pi }=\dfrac{112+28\pi -28\pi }{4+\pi }=\dfrac{112}{4+\pi }\]
\[\therefore \] on solving answers are the same.
Here, the area is minimum at \[x=\dfrac{28\pi }{4+\pi }\].