Question

A wire of resistance $10 ohm$ is bent in the form of a closed circle. What is the effective resistance between the two points at the end of any diameter of the circle?
A. $0.4 ohm$
B. $0 ohm$
C. $2.5 ohm$
D. $10 ohm$

Answer 1

Hint: Find the resistances of the two half sections of the circular wire with the help of the formula for the resistance of a wire. Then use the formula for the effective resistance of two resistance in parallel connection.

Formula used:
$R=\dfrac{\rho l}{A}$
$\Rightarrow \dfrac{1}{{{R}_{eff}}}=\dfrac{1}{{{R}_{1}}}+\dfrac{1}{{{R}_{2}}}$

Complete step by step answer:
It is given that a wire of resistance 10 ohm is bent in the form of a closed circle. Now, if the points at both the ends of a diameter of that circle is taken into consideration, it will behave as two different resistances in parallel connection.

Let the two resistances be ${{R}_{1}}$ and ${{R}_{2}}$. Now, draw a circuit with the two resistances in parallel connection as shown in the figure.

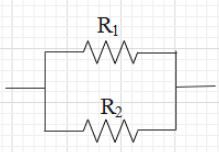
Let us first find the values of ${{R}_{1}}$ and ${{R}_{2}}$. For this will use the formula for resistance of a conducting wire, i.e. $R=\dfrac{\rho l}{A}$ ,
where $\rho $ is the resistivity of the material of the wire, l is the length and A is the cross sectional area of the wire.

It is given that the resistance of the wire is 10 ohm.
$\Rightarrow \dfrac{\rho l}{A}=10$ …. (i)
Since the two resistances are of the same wire, $\rho $ is the same for both the sections of the wire.

Let us assume that the wire has a uniform cross section. Therefore, the cross section area of both the sections will be equal. Since we have divided the circle across the diameter, the length of the two sections will be $\dfrac{l}{2}$.
Therefore,
$\Rightarrow {{R}_{1}}=\dfrac{\rho \left( \dfrac{l}{2} \right)}{A}=\dfrac{1}{2}\left( \dfrac{\rho l}{A} \right)$ …. (ii).
And
${{R}_{2}}=\dfrac{\rho \left( \dfrac{l}{2} \right)}{A}=\dfrac{1}{2}\left( \dfrac{\rho l}{A} \right)$ …. (iii).
From (i), (ii) and (iii) we get that ${{R}_{1}}={{R}_{2}}=\dfrac{10}{2}=5ohm$.

This means that the circuit has two resistances of 5 ohms connected in parallel connection.
When two resistances ${{R}_{1}}$ and ${{R}_{2}}$ are in parallel connected, the effective resistance of the circuit is given as $\dfrac{1}{{{R}_{eff}}}=\dfrac{1}{{{R}_{1}}}+\dfrac{1}{{{R}_{2}}}$ …. (iv),
where ${{R}_{eff}}$ is the effective resistance.
Substitute the values of ${{R}_{1}}$ and ${{R}_{2}}$ in (iv).
$\Rightarrow \dfrac{1}{{{R}_{eff}}}=\dfrac{1}{5}+\dfrac{1}{5}=\dfrac{2}{5}$
$\therefore {{R}_{eff}}=\dfrac{5}{2}=2.5ohm$.
Therefore, the effective resistance between the two points at the end of any diameter of the circle is $2.5ohm$.

Hence, the correct option is C.

Note:We can also say that for a given wire, its resistance is directly proportional to its length but inversely proportional to the area of its cross section. Therefore, if the wire has constant or uniform cross sectional area then its resistance will only depend on its length. If the length reduces to half of the initial length then its resistance reduces to half of the initial value.