
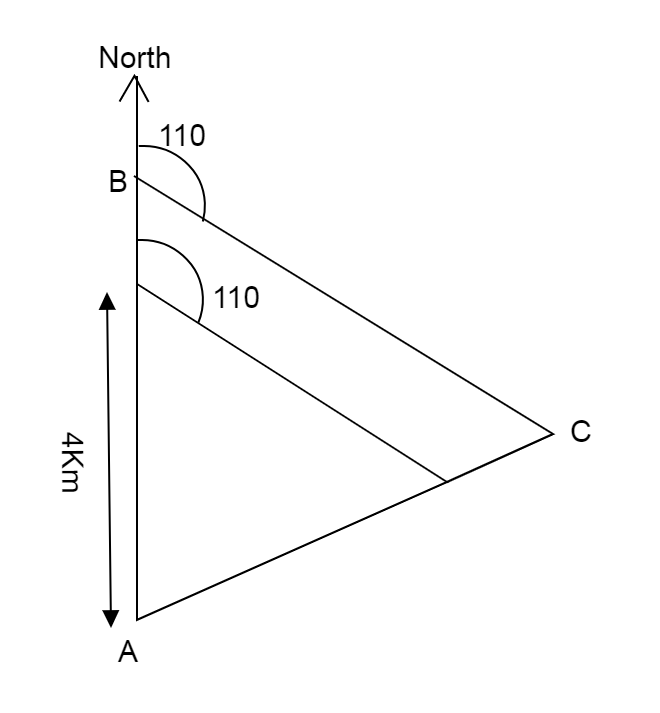
AB = BC = 6Km. Junior students follow a similar path but they only walk 4Km North from A, then 4Km on a bearing
Senior students walk to a total of 18.9Km
Calculate the distance walked by junior students.

Answer
452.4k+ views
1 likes
Hint: Since the bigger triangle represents the path covered by senior students and the smaller triangle represents the path covered by junior students. We use the given sides of the triangle given and the total distance covered by senior students to calculate the missing side of the triangle. Use the exterior angle property to calculate the opposite angles along with the property of isosceles triangle in smaller triangles. Now we calculate the length of the third side using sine law.
* Exterior angle of a triangle is equal to the sum of opposite interior angles of the triangle.
* Law of sine states that in a triangle ABC the ratio of side of a triangle to the sine of opposite angle is same for all the sides of the triangle, i.e. if side a has opposite angle A, side b has opposite angle B and side c has opposite angle C, then we can write
* Isosceles triangle has two sides of equal length and the angles opposite to equal sides are equal in measure.
Complete step by step answer:
We firstly name the third point of the smaller triangle formed as D
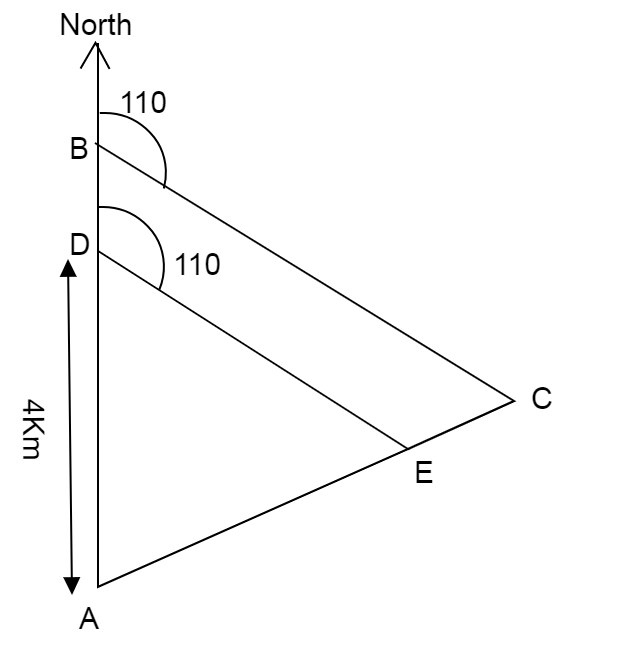
We are given that senior students travel from A to B and then B to C and back from C to A.
So the total distance covered by senior students is perimeter of triangle ABC.
We are given
Now we apply the formula of perimeter of triangle i.e. sum of all three sides of triangle.
Substitute the values of
Shift all constant values to RHS
We are given that junior students travel from A to D and then D to E and back from E to A.
So the total distance covered by senior students is the perimeter of triangle ADE.
We are given junior students follow a similar path but 4Km to north and then 4Km after turning
i.e.
Substitute the values of
Now we know
Apply property of exterior angles to the
Substitute the value of
Now we know
Divide both sides by 2
Cancel same factors from numerator and denominator on both sides of the equation
Then
Since
Substitute the value of
Shift all constant values to RHS of the equation
Now we draw the triangle ADE with all its dimensions
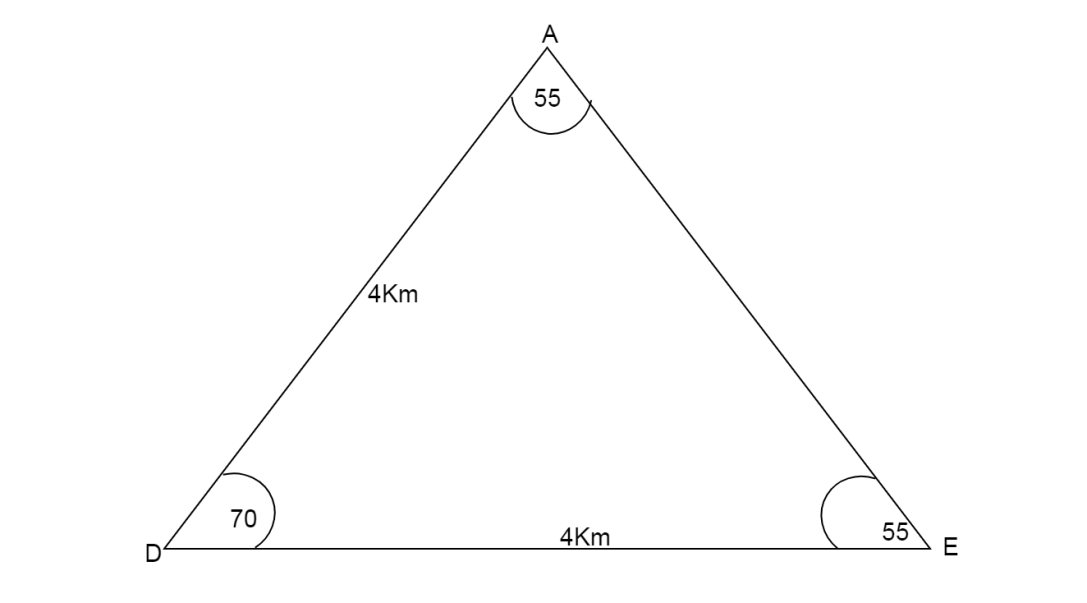
Now we apply sine rule in triangle ABD,
Substitute the values of sides and angles.
Now we equate last two fractions
Substitute the value of
Cancel the same factors and divide the numerator by denominator.
Substitute the value of EA in equation (2)
Note: Many students make the mistake of solving for the value of the third side of the triangle by constructing an altitude and then applying Pythagoras theorem which is a long procedure, instead students can opt for sine rule. Also, while calculating the sum of opposite angles in exterior angles property always take the angles that are on opposite edges to that of the given edge of exterior angle.
* Exterior angle of a triangle is equal to the sum of opposite interior angles of the triangle.
* Law of sine states that in a triangle ABC the ratio of side of a triangle to the sine of opposite angle is same for all the sides of the triangle, i.e. if side a has opposite angle A, side b has opposite angle B and side c has opposite angle C, then we can write
* Isosceles triangle has two sides of equal length and the angles opposite to equal sides are equal in measure.
Complete step by step answer:
We firstly name the third point of the smaller triangle formed as D

We are given that senior students travel from A to B and then B to C and back from C to A.
So the total distance covered by senior students is perimeter of triangle ABC.
We are given
Now we apply the formula of perimeter of triangle i.e. sum of all three sides of triangle.
Substitute the values of
Shift all constant values to RHS
We are given that junior students travel from A to D and then D to E and back from E to A.
So the total distance covered by senior students is the perimeter of triangle ADE.
We are given junior students follow a similar path but 4Km to north and then 4Km after turning
i.e.
Substitute the values of
Now we know
Apply property of exterior angles to the
Substitute the value of
Now we know
Divide both sides by 2
Cancel same factors from numerator and denominator on both sides of the equation
Then
Since
Substitute the value of
Shift all constant values to RHS of the equation
Now we draw the triangle ADE with all its dimensions

Now we apply sine rule in triangle ABD,
Substitute the values of sides and angles.
Now we equate last two fractions
Substitute the value of
Cancel the same factors and divide the numerator by denominator.
Substitute the value of EA in equation (2)
Note: Many students make the mistake of solving for the value of the third side of the triangle by constructing an altitude and then applying Pythagoras theorem which is a long procedure, instead students can opt for sine rule. Also, while calculating the sum of opposite angles in exterior angles property always take the angles that are on opposite edges to that of the given edge of exterior angle.
Latest Vedantu courses for you
Grade 10 | MAHARASHTRABOARD | SCHOOL | English
Vedantu 10 Maharashtra Pro Lite (2025-26)
School Full course for MAHARASHTRABOARD students
₹31,500 per year
Recently Updated Pages
Express the following as a fraction and simplify a class 7 maths CBSE

The length and width of a rectangle are in ratio of class 7 maths CBSE

The ratio of the income to the expenditure of a family class 7 maths CBSE

How do you write 025 million in scientific notatio class 7 maths CBSE

How do you convert 295 meters per second to kilometers class 7 maths CBSE

Write the following in Roman numerals 25819 class 7 maths CBSE

Trending doubts
Where did Netaji set up the INA headquarters A Yangon class 10 social studies CBSE

A boat goes 24 km upstream and 28 km downstream in class 10 maths CBSE

Why is there a time difference of about 5 hours between class 10 social science CBSE

The British separated Burma Myanmar from India in 1935 class 10 social science CBSE

The Equation xxx + 2 is Satisfied when x is Equal to Class 10 Maths

What are the public facilities provided by the government? Also explain each facility




