Question

ABC is an isosceles triangle inscribed in a circle. If \[AB=AC=12\sqrt{5}cm\] and \[BC=24cm\], find the radius of the circle.

Answer 1

Hint: In this type of question we have to use the concept of the basic properties of the circle and Pythagoras theorem. We will first draw an isosceles triangle inside a circle and then by using properties of the circle and Pythagoras theorem we can find the radius of the circle.

Complete step by step answer:
Now, we have to find the radius of the circle such that, ABC is an isosceles triangle inside the circle where \[AB=AC=12\sqrt{5}cm\] and \[BC=24cm\].

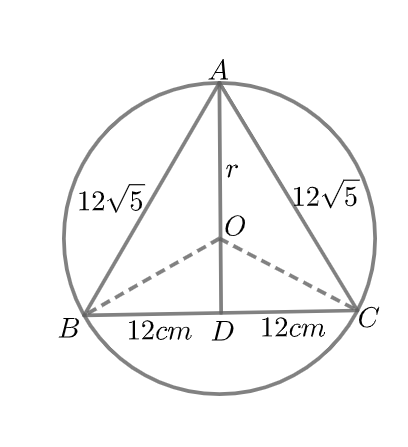
Now, we will join \[OB,OC\] and \[OA\]. Also we draw \[AD\bot BC\] which passes through the centre of the circle \[O\] and \[OD\] bisects \[BC\] in \[D\].
\[\Rightarrow BD=CD=12cm\]
Hence, we get a right angled triangle \[\Delta ABD\].
Thus by using Pythagoras theorem we can write,
\[\Rightarrow A{{B}^{2}}=A{{D}^{2}}+B{{D}^{2}}\]
By substituting the values we get,
\[\begin{align}
  & \Rightarrow {{\left( 12\sqrt{5} \right)}^{2}}=A{{D}^{2}}+{{\left( 12 \right)}^{2}} \\
 & \Rightarrow 144\times 5=A{{D}^{2}}+144 \\
 & \Rightarrow 720=A{{D}^{2}}+144 \\
 & \Rightarrow 720-144=A{{D}^{2}} \\
 & \Rightarrow 576=A{{D}^{2}} \\
\end{align}\]
Taking square root of both sides we get,
\[\begin{align}
  & \Rightarrow \sqrt{576}=AD \\
 & \Rightarrow 24cm=AD \\
\end{align}\]
Let us suppose that the radius of the circle \[OA=OB=OC=r\],
\[\begin{align}
  & \Rightarrow OD=AD-AO \\
 & \Rightarrow OD=24-r \\
\end{align}\]
By using Pythagoras theorem for right angled triangle \[\Delta OBD\],
\[\begin{align}
  & \Rightarrow O{{B}^{2}}=B{{D}^{2}}+O{{D}^{2}} \\
 & \Rightarrow {{r}^{2}}={{\left( 12 \right)}^{2}}+{{\left( 24-r \right)}^{2}} \\
 & \Rightarrow {{r}^{2}}=144+576-48r+{{r}^{2}} \\
 & \Rightarrow 0=720-48r \\
 & \Rightarrow 720=48r \\
 & \Rightarrow \dfrac{720}{48}=r \\
 & \Rightarrow 15cm=r \\
\end{align}\]
Hence, the radius of the circle is 15 cm.

Note: In this type of question students have to draw proper figures regarding the statements given in the question. Also students have to draw lines joining the centre to the vertices of the triangle to get the radius of the circle. Then students have to use the Pythagoras theorem to find the required value. Students have to take care when they calculate the square of \[\left( 12\sqrt{5} \right)\]. Also students have to use the formula \[{{\left( a-b \right)}^{2}}={{a}^{2}}-2ab+{{b}^{2}}\] for the expansion of \[{{\left( 24-r \right)}^{2}}\].