
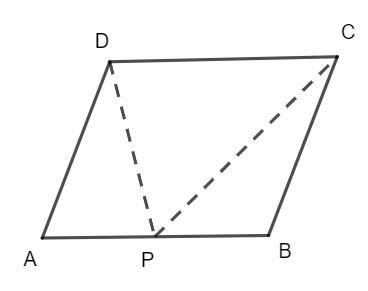
ABCD is a parallelogram as shown in the figure. If AB = 2AD and P is midpoint of AB, then what is the value of \[\angle CPD\] ?
(a). 90°
(b). 60°
(c). 45°
(d). 135°

Answer
604.5k+ views
Hint: Use the property of the parallelogram that the adjacent angles are supplementary. Then find the angle CPD in terms of the adjacent angles and find its value.
Complete step-by-step answer:
ABCD is a parallelogram, hence, the adjacent angles of the parallelogram are supplementary, that is, the sum of angles is 180°.
\[\angle A + \angle B = 180^\circ ............(1)\]
It is given that AB = 2 AD, then we have:
\[AD = \dfrac{{AB}}{2}..............(2)\]
It is given that P is the midpoint of AB. Then, we have the following:
\[AP = \dfrac{{AB}}{2}..........(3)\]
From equation (2) and equation (3), we have:
\[AD = AP\]
Hence, the triangle APD is an isosceles triangle.
The sum of the angles of the triangle APD is 180°.
\[\angle APD + \angle ADP + \angle A = 180^\circ \]
\[2\angle APD + \angle A = 180^\circ \]
Solve for the angle APD to get as follows:
\[\angle APD = 90^\circ - \dfrac{{\angle A}}{2}............(4)\]
The opposite sides of the parallelogram are equal. Hence, AD = BC, then we have:
\[BP = BC\]
Then, the triangle BPC is also an isosceles triangle.
The sum of the angles of the triangle BPC is 180°.
\[\angle BPC + \angle BCP + \angle B = 180^\circ \]
\[2\angle BPC + \angle B = 180^\circ \]
Solve for the angle BPC to get as follows:
\[\angle BPC = 90^\circ - \dfrac{{\angle B}}{2}............(5)\]
The angle on a straight line add up to 180°, then we have on line APB as follows:
\[\angle BPC + \angle CPD + \angle APD = 180^\circ \]
Using equations (4) and (5), we get:
\[90^\circ - \dfrac{{\angle B}}{2} + \angle CPD + 90^\circ - \dfrac{{\angle A}}{2} = 180^\circ \]
Simplifying, we have:
\[180^\circ - \dfrac{{\angle B + \angle A}}{2} + \angle CPD = 180^\circ \]
Canceling 180° on both sides, we have:
\[\angle CPD = \dfrac{{\angle B + \angle A}}{2}\]
From equation (1), we have:
\[\angle CPD = \dfrac{{180^\circ }}{2}\]
\[\angle CPD = 90^\circ \]
Hence, the correct answer is option (a).
Note: You can also find the angles CDP and DCP in terms of the angle D and angle C respectively and then find the angle CPD using the properties of the triangle.
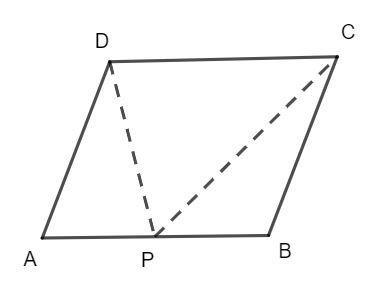
Complete step-by-step answer:

ABCD is a parallelogram, hence, the adjacent angles of the parallelogram are supplementary, that is, the sum of angles is 180°.
\[\angle A + \angle B = 180^\circ ............(1)\]
It is given that AB = 2 AD, then we have:
\[AD = \dfrac{{AB}}{2}..............(2)\]
It is given that P is the midpoint of AB. Then, we have the following:
\[AP = \dfrac{{AB}}{2}..........(3)\]
From equation (2) and equation (3), we have:
\[AD = AP\]
Hence, the triangle APD is an isosceles triangle.
The sum of the angles of the triangle APD is 180°.
\[\angle APD + \angle ADP + \angle A = 180^\circ \]
\[2\angle APD + \angle A = 180^\circ \]
Solve for the angle APD to get as follows:
\[\angle APD = 90^\circ - \dfrac{{\angle A}}{2}............(4)\]
The opposite sides of the parallelogram are equal. Hence, AD = BC, then we have:
\[BP = BC\]
Then, the triangle BPC is also an isosceles triangle.
The sum of the angles of the triangle BPC is 180°.
\[\angle BPC + \angle BCP + \angle B = 180^\circ \]
\[2\angle BPC + \angle B = 180^\circ \]
Solve for the angle BPC to get as follows:
\[\angle BPC = 90^\circ - \dfrac{{\angle B}}{2}............(5)\]
The angle on a straight line add up to 180°, then we have on line APB as follows:
\[\angle BPC + \angle CPD + \angle APD = 180^\circ \]
Using equations (4) and (5), we get:
\[90^\circ - \dfrac{{\angle B}}{2} + \angle CPD + 90^\circ - \dfrac{{\angle A}}{2} = 180^\circ \]
Simplifying, we have:
\[180^\circ - \dfrac{{\angle B + \angle A}}{2} + \angle CPD = 180^\circ \]
Canceling 180° on both sides, we have:
\[\angle CPD = \dfrac{{\angle B + \angle A}}{2}\]
From equation (1), we have:
\[\angle CPD = \dfrac{{180^\circ }}{2}\]
\[\angle CPD = 90^\circ \]
Hence, the correct answer is option (a).
Note: You can also find the angles CDP and DCP in terms of the angle D and angle C respectively and then find the angle CPD using the properties of the triangle.
Recently Updated Pages
What happens to glucose which enters nephron along class 10 biology CBSE

Write a dialogue with at least ten utterances between class 10 english CBSE

A circle is inscribed in an equilateral triangle and class 10 maths CBSE

When the JanmiKudian Act was passed that granted the class 10 social science CBSE

A sector containing an angle of 120 circ is cut off class 10 maths CBSE

The sum of digits of a two digit number is 13 If t-class-10-maths-ICSE

Trending doubts
The shortest day of the year in India

Why is there a time difference of about 5 hours between class 10 social science CBSE

Write a letter to the principal requesting him to grant class 10 english CBSE

What is the median of the first 10 natural numbers class 10 maths CBSE

The Equation xxx + 2 is Satisfied when x is Equal to Class 10 Maths

What is the missing number in the sequence 259142027 class 10 maths CBSE




