Question

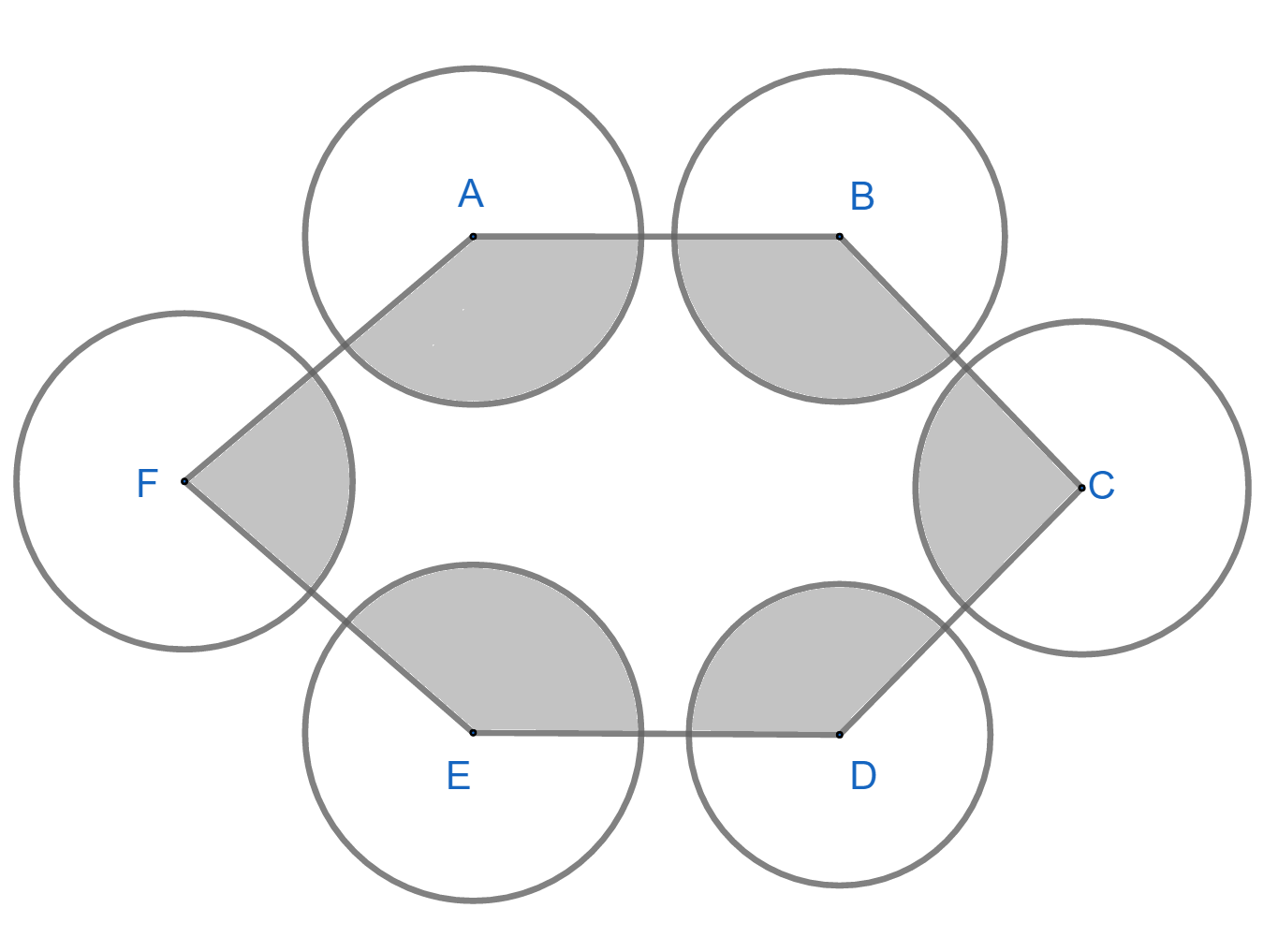
ABCDEF is a regular hexagon with vertices A, B, C, D, E and F as the center, circle of same radius r are drawn. Find the area of the shaded portion in figure.

Answer 1

Hint: At first, we will use formula for finding interior angles of a regular polygon which is given by: each interior angle of regular polygon $\Rightarrow \dfrac{2n-4}{n}\times {{90}^{\circ }}$ where n is the number of sides of the given regular polygon. After that, we will calculate the area of the portion of one circle inside the hexagon by using interior angle. At last we will calculate the area of the portion of all six circles inside the hexagon.

Complete step-by-step answer:
Here, we are given a regular hexagon which is a polygon with 6 sides. As we know, each interior angle of regular polygon is given by $\Rightarrow \dfrac{2n-4}{n}\times {{90}^{\circ }}$ where n is the number of sides of polygon. As n = 6 for hexagon, therefore, every interior angle of hexagon \[\Rightarrow \dfrac{2\left( 6 \right)-4}{6}\times {{90}^{\circ }}={{120}^{\circ }}\]
Since, every vertex of the hexagon acts as a center for circles with radius r. Therefore, exactly ${{120}^{\circ }}$ portion of each circle lies inside the hexagon which we have to calculate.
As we know, the area of a circle represents ${{360}^{\circ }}$. So, we will calculate the area of one circle which represents ${{120}^{\circ }}$ portion of the circle, using a unitary method.
For ${{360}^{\circ }}$ area of 1 circle $\Rightarrow \pi {{r}^{2}}$
For ${{1}^{\circ }}$ area of 1 circle $\Rightarrow \dfrac{\pi {{r}^{2}}}{{{360}^{\circ }}}$
For ${{120}^{\circ }}$ area of 1 circle $\Rightarrow \dfrac{\pi {{r}^{2}}}{{{360}^{\circ }}}\times {{120}^{\circ }}=\dfrac{\pi {{r}^{2}}}{3}$
Here, we are given that, every vertex has a circle, therefore, we have to find area of six circles which will be equal to $\Rightarrow 6\times \dfrac{\pi {{r}^{2}}}{3}=2\pi {{r}^{2}}$
Hence, a portion of six circles inside the regular hexagon will be given by $2\pi {{r}^{2}}$.
Therefore, total shaded area $\Rightarrow 2\pi {{r}^{2}}$

Note: Students should take care while calculating interior angle of the regular hexagon using the formula. This question is tricky at points where we have to find the area of the portion of the circle inside the hexagon only, so students should carefully understand the concept. Formulas for finding the area of a circle should also be kept in mind as it is for ${{360}^{\circ }}$.