Question

ABCDEFGH is a cuboid. Find EG.

Answer 1

Hint: If we consider the triangle formed by EGH, $\angle EGH=90{}^\circ $, EG will be the hypotenuse, we can get the length of EH as we know the length of FG and we also know the length of HG. By applying the formula $''{{\left( hypotenuse \right)}^{2}}={{\left( side1 \right)}^{2}}+{{\left( side2 \right)}^{2}}''$in $\Delta EHG$, we will get the length of EG.

Complete step-by-step answer:

A cuboid is defined as a solid which has six rectangular faces at right angles to each other.
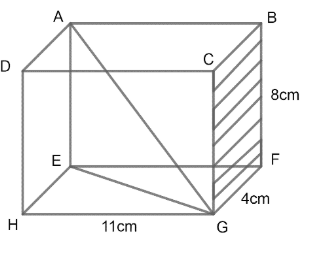
We have to find the length of EG. For this let us consider the triangle formed by EHG.

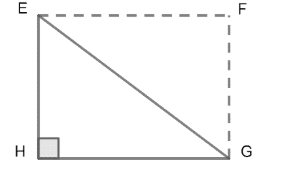
We know that all the faces of a cuboid are rectangular. So, quadrilateral HEFG will also be a rectangle. We can observe in the above diagram that $\angle EHG$ is one corner of the rectangle HEFG. Hence, $\angle EHG=90{}^\circ $.
So, $\Delta EHG$ will be a right triangle with $\angle EHG=90{}^\circ $and EG is the hypotenuse of this right triangle.
We know, $''{{\left( hypotenuse \right)}^{2}}={{\left( side1 \right)}^{2}}+{{\left( side2 \right)}^{2}}''$
${{\left( EG \right)}^{2}}={{\left( HE \right)}^{2}}+{{\left( HG \right)}^{2}}...............\left( 1 \right)$
To find the length of the hypotenuse (i.e. EG), we need to find the length of other two sides;
HG = 11 cm (Given in the diagram of the question)
We know, that the opposite sides of a rectangle are same so for rectangle HEFG, HE = FG

And FG = 4 cm (Given in the diagram of the question)
So, HE = 4 cm.
Now, on putting HE = 4 cm and HG = 11 cm in equation (1),
We will get;
\[\begin{align}
  & {{\left( EG \right)}^{2}}={{\left( 4cm \right)}^{2}}+{{\left( 11cm \right)}^{2}} \\
 & \Rightarrow {{\left( EG \right)}^{2}}=16c{{m}^{2}}+121c{{m}^{2}} \\
 & \Rightarrow {{\left( EG \right)}^{2}}=137c{{m}^{2}} \\
\end{align}\]
Taking positive square root both sides, we will get;
$\Rightarrow EG=\pm \sqrt{137}cm$
We have taken positive square roots because the length of the side cannot be negative.
$\Rightarrow EG=11.70cm$
Hence, the required length of the EG = 11.70 cm.

Note: Another method;
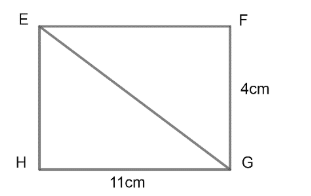
We can calculate the length of EG by considering the rectangle HEFG. EG is a diagonal of the rectangle.

 Formula:
$\left( \text{length}\ \text{of}\ \text{diagonal }\text{of}\ \text{a}\ \text{rectangle} \right)=\sqrt{{{a}^{2}}+{{b}^{2}}}$
Where ‘a’ and ‘b’ is its length and breadth.
\[\Rightarrow EG=\sqrt{{{\left( 4cm \right)}^{2}}+{{\left( 11cm \right)}^{2}}}\]
\[\begin{align}
  & =\sqrt{137}cm \\
 & =11.70cm \\
\end{align}\]