Question

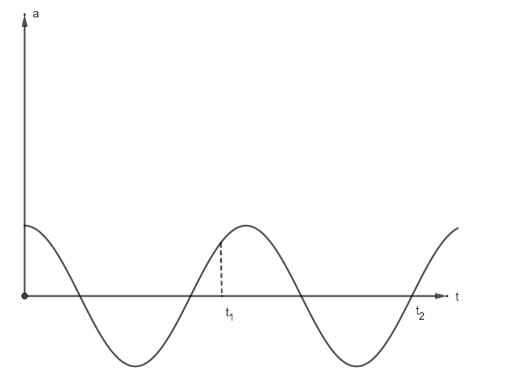
Acceleration-time graph of a particle in SHM is as shown in figure. Match the following two columns.

List 1	List 2
(a) Displacement of particle at ${t_1}$	(p) Zero
(b) Displacement of particle at ${t_2}$	(q) Positive
(c) Velocity of particle at ${t_1}$	(r) Negative
(d) Velocity of particle at ${t_2}$	(s) maximum

Answer 1

Hint:To solve questions of SHM related to graphs we need to know the basic formulas of SHM and then apply the concept related to the graph. The formulas required here are acceleration, velocity, displacement, and time-related formulas. We also need to understand seeing the graph, when the gradient is positive and when negative at a given point.

Complete step by step answer:
Let's examine the $1^{st}$ question: We see from the graph that at ${t_1}$, acceleration is positive, hence by the formula of acceleration: $a = - {\omega ^2}x$, we see that the value of $x$ is negative. Hence option (r).
$2^{nd}$ question: At the time ${t_2}$, we see that acceleration is zero, hence the value of displacement also is zero. Hence option (p).

$3^{rd}$ question: We know acceleration is the rate of change of velocity, let's use that: $v = \int {adt} $, from $0$ time to ${t_1}$ we see that the area of a-t curve is more negative, thus we can say that $v$ is negative.Hence option (r).
$4^{th}$ question: Here we see that ${t_2}$ is in mean position, thus displacement is zero and acceleration is moving from negative to a positive value, ( initially at zero) , hence we can say that the value of displacement is going from positive to negative as $a = - {\omega ^2}x$ and so does its velocity. Also, we know that for a particle performing SHM, it has a maximum speed at mean position. Hence the answer should be both (r) negative and (s)maximum.

Note:To solve these questions the basic concept of SHM should be known like when is the displacement positive, how is the direction of acceleration and displacement related, what is the value of maximum amplitude, etc. Knowing these would make the problem very easy.