Question

According to the quantum theory, a photon of electromagnetic radiation of frequency $\nu$ has energy $E=h\nu$ where h is the Planck’s constant. According to the theory of relativity, a particle of mass m has equivalent energy $E = mc^2$, where c is the speed of light. Thus, a photon can be treated as a particle having effective mass $m=\dfrac{h\nu}{c^2}$. If a flash of light is sent horizontally in earth’s gravitational field, then photons while travelling a horizontal distance d would fall through a distance given by:
A.$\dfrac{gd^2}{2c^2}$
B.$\dfrac{h}{mc}$
C.$\dfrac{mcd^2}{h}$
D.Zero

Answer 1

Hint: First identify the kind of motion that the photon is subjected to. In other words, we see that the photon undergoes the trajectory of a projectile. Then, find the time taken by the photon to hit the ground at a horizontal distance d. Now, this is the same amount of time that you need to consider to calculate the distance which the photon falls through. Use a kinematic equation of motion in the picture of gravity to obtain the final expression. Do not forget that the photon possesses no initial velocity in the vertical direction.

Formula Used:
Distance travelled in the vertical direction $s = u_y t +\dfrac{1}{2}gt^2$

Complete answer:
We know that a photon is an elementary particle that is a carrier of electromagnetic field or radiation. They are massless particles in sense that their mass is zero at zero momentum. They always move at the speed of light c in free space and are the basic units of all mass. This property is also known as the invariant mass and remains independent of overall momentum.
We are given that the energy possessed by a photon is given as $E = h\nu$.
But from the mass-energy equivalence principle which states that a body in motion possesses relativistic mass that can be derived from its total energy divided by the speed of light squared, we see that energy possessed by a photon in motion can be quantified as:
$E = mc^2$
Equating the two energy equations we get:
$\Rightarrow h\nu = mc^2 \Rightarrow m = \dfrac{h\nu}{c^2}$
Let the photons fall through a distance s when a horizontal flash of light is sent through the earth’s gravitational field.

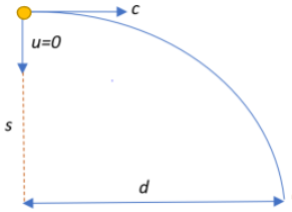
The photons follow the kinematics of a projectile motion.
The photons travel with a horizontal velocity of c but have no vertical velocity associated with their motion. Therefore, $u_x = c$ and $u_y = 0$
If the horizontal distance travelled by a photon following this trajectory is $d_x = d$, then the time it takes to travel this distance is given by:
$t =\dfrac{d_x}{u_x} = \dfrac{d}{c}$
Therefore, the distance through which the photon would fall vertically downwards in this time can be given by the kinematic equation of motion:
$h_y = u_y t+ \dfrac{1}{2}gt^2$
$\Rightarrow s = 0 + \dfrac{1}{2}gt^2$
$s = \dfrac{1}{2}g.\left(\dfrac{d}{c}\right)^2 = \dfrac{gd^2}{2c^2}$

Therefore, the correct option would be A. $\dfrac{gd^2}{2c^2}$.

Note:
Remember that we say photons are massless particles only in the quantum theoretical aspect and we assume they have a mass proportional to their energy in accordance with the mass-energy equivalence principle. The lack of mass only pertains to the rest mass which means that it is only a photon that is at rest that possesses no energy and hence no momentum or mass. However, according to the special theory of relativity, photons are never at rest and hence possess zero rest mass, possess energy and consequently equivalent mass.
While it stands true that photons have no mass, we see that gravity influences the path of photons, which is given in the question as well. This, however, is not because gravity pulls on photons directly but because it pulls on the space-time that warps the mass that photons travel through.