Question

How many acute angles are there in a regular polygon?
(A). 2
(B). 0
(C). 3
(D). 4

Answer 1

Use the formula Sum of angles of a regular polygon = (n – 2) \[180{}^\circ \] to find the sum of all the internal angles of a pentagon and then equate it with the sum of angles. Use the condition i.e. “all the angles of a regular pentagon are the same” and solve the equation to get the final answer.

Complete step-by-step solution -
To solve the given question we will first draw a regular pentagon so that we can solve it easily, therefore,

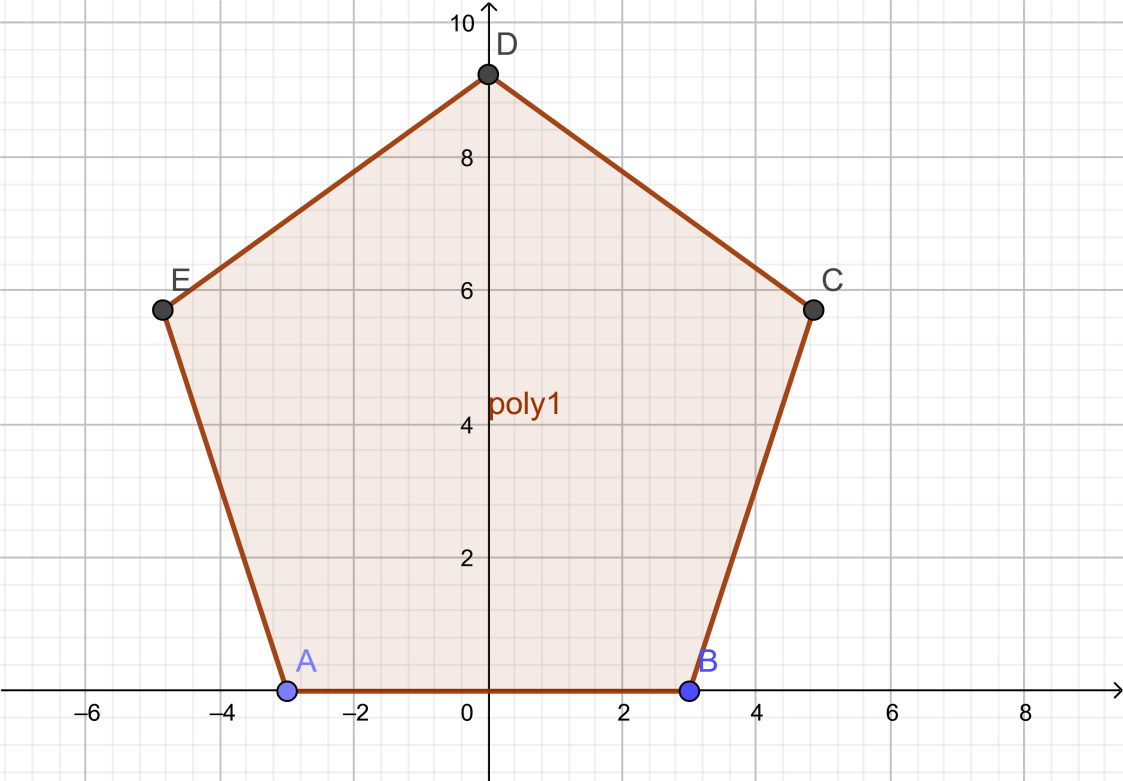
As we have a regular pentagon with five sides and five angles.
Before we find the measure of angles; we should first find out the sum of angles of a pentagon.
Number of sides of a pentagon = 5 ……………………………………………………… (1)
To proceed further in the solution we should know the formula given below,
Formula:
Sum of angles of a regular polygon = (n – 2) \[180{}^\circ \]
If we substitute the value of equation (1) in the above formula we will get,
Sum of angles of a regular pentagon = (5 – 2) \[180{}^\circ \]
Therefore, Sum of angles of a regular pentagon = \[3\times 180{}^\circ \]
Therefore, Sum of angles of a regular pentagon = \[540{}^\circ \]
If we refer the above figure and write the angles, we will get,
$\therefore \angle A+\angle B+\angle C+\angle D+\angle E=540{}^\circ $ ………………………………………………………. (2)
Now, as we all know that all the angles of a regular pentagon are equal therefore from figure we can write, $\angle A=\angle B=\angle C=\angle D=\angle E$
Therefore the above equation will become,
$\therefore \angle A+\angle A+\angle A+\angle A+\angle A=540{}^\circ $
$\therefore 5\angle A=540{}^\circ $
$\therefore \angle A=\dfrac{540{}^\circ }{5}$
$\therefore \angle A=108{}^\circ $
Therefore, we can write,
$\therefore \angle A=\angle B=\angle C=\angle D=\angle E=108{}^\circ $
Now we know that acute angle is always less than $90{}^\circ $ and from the above equation it is clear that none of the angles of a pentagon is less than $90{}^\circ $.
Therefore, there are zero acute angles in a regular pentagon.
Therefore, the correct answer is option (b).

Note: Many students take the sum of pentagon as $360{}^\circ $ because they are in a hurry while writing the exam and therefore results in the wrong answer. Therefore do remember the formula Sum of angles of a regular polygon = (n – 2) \[180{}^\circ \] so that you can get the sum of angles of any pentagon.