Question

(A)Draw a circuit diagram of transistor as an amplifier in common emitter configuration.
(B) Obtain the expression for the voltage gain.

Answer 1

Hint: First of all, we will draw the circuit diagram and then using that circuit diagram we will find the input and output voltage. Now, the ratio of output voltage and input voltage Is voltage gained which can be expressed mathematically as, ${{A}_{v}}=\dfrac{\text{output}\ \text{voltage}}{\text{input}\ \text{voltage}}$. Using this expression, we will find the solution.

Formula used: ${{A}_{v}}=\dfrac{\text{output}\ \text{voltage}}{\text{input}\ \text{voltage}}$

Complete step by step answer:
Before drawing the circuit diagram we will understand what transistors are, so, a transistor is a semiconductor device which is used to amplify or switch electronic signals and electrical power. It is made up of semiconductor material and it usually has at least three terminals i.e. Base, Collector and Emitter, for connection to an external circuit.

Now, in the question we are asked to draw the circuit diagram of a transistor as an amplifier in common emitter common configuration, which is shown in the figure below,

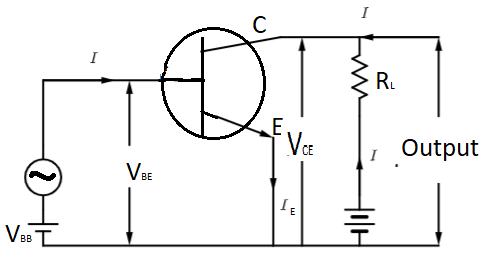
Where, ${{I}_{B}}$ is base current, ${{I}_{E}}$ is emitter current, ${{I}_{C}}$ is collector current, ${{V}_{BE}}$ is voltage difference between base and emitter, ${{V}_{CE}}$ is voltage difference between collector and emitter ${{V}_{BB}}$ is base power supply and ${{V}_{CC}}$ is collector power supply.

Now, from the circuit diagram it can be seen that the input voltage is ${{V}_{BE}}$. Now, we know that $V=IR$,

Where, I is current and R is resistance, so, applying the same in ${{V}_{BE}}$ we will get,
 ${{V}_{BE}}={{I}_{B}}{{R}_{in}}$ …………………(i)

Now, same way the output voltage is ${{V}_{CE}}$ and it can be written as,
${{V}_{CE}}={{I}_{C}}{{R}_{out}}$ ………………..(ii)

Now, the voltage gain is given by,

${{A}_{v}}=\dfrac{\text{output}\ \text{voltage}}{\text{input}\ \text{voltage}}$
So, now substituting the values of input and output voltages in above equation we will get,
${{A}_{v}}=\dfrac{\text{output}\ \text{voltage}}{\text{input}\ \text{voltage}}$

${{A}_{v}}=\dfrac{{{V}_{CE}}}{{{V}_{BE}}}=\dfrac{\left( {{I}_{C}} \right){{R}_{out}}}{\left( {{I}_{B}} \right){{R}_{in}}}$ …………………….(iii)

Now, $\dfrac{{{I}_{C}}}{{{I}_{B}}}$ is called current gain which can be given as ${{\beta }_{AC}}$, so substituting it in expression (iii) we will get,

${{A}_{v}}={{\beta }_{AC}}\dfrac{{{R}_{out}}}{{{R}_{in}}}$.

Thus, voltage gain can be given by, ${{A}_{v}}={{\beta }_{AC}}\dfrac{{{R}_{out}}}{{{R}_{in}}}$.

Note: Students might make mistake in considering the input and output voltage as ${{V}_{BE}}$ and ${{V}_{CE}}$, instead of that they might consider the ${{V}_{BB}}$ and ${{V}_{CC}}$ as input and output voltages and due to that the answer will be wrong. So, students must take care while solving such problems.