Question

a)Draw the ray diagram showing the formation of an image by a compound microscope.
b) Show that in order to achieve large magnification in a compound microscope the magnitude of the focal length of objective and the eyepiece should be small.

Answer 1

Hint: To draw the ray diagram of the compound microscope, it basically consists of two convex lenses namely the objective that is kept near the specimen and the eyepiece that is kept at our least distance of distinct vision. While drawing the ray diagram it is to be considered the image formed by the objective lies within the focal length of the eyepiece and the focal length of the eyepiece is greater than that of the objective. Further will obtain an expression for magnification power and verify whether to increase magnification the focal length of the either lenses should be reduced.

Complete step by step answer:
The ray diagram of a compound microscope is shown below in Fig 1.

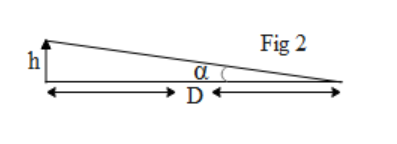
The magnifying power of the lens is defined as the ratio of the angle subtended by the image at the eye i.e. $\text{ }\!\!\beta\!\!\text{ }$ (as seen in Fig 1)to the angle subtended by the object at the eyepiece i.e. $\text{ }\!\!\alpha\!\!\text{ }$. (as seen in Fig 2) Mathematically written as,
The angular magnification of the image is given by, $m=\dfrac{\begin{align}
  & \text{Angle Subtended by the image at least } \\
 & \text{at the eyepiece} \\
\end{align}}{\begin{align}
  & \text{Angle Subtended by the object at least } \\
 & \text{at the eyepiece} \\
\end{align}}$
For small angle $\tan \theta \simeq \theta $ Hence, we can write the above equation as $m=\dfrac{\tan \beta }{\tan \alpha }$
From trigonometric definition of $\tan \theta $ we can write the above equation as,
$m=\dfrac{\dfrac{\text{height of the image }}{\text{-N}}}{\dfrac{\text{height of the object}}{-D}}=\dfrac{{{\text{h}}_{\text{I}}}}{\text{N}}\times \dfrac{\text{D}}{\text{h}}={{M}_{O}}{{M}_{E}}....(1)$
Where ${{M}_{O}}$is the magnification produced by the objective and ${{M}_{E}}$is the magnification produced by the eye piece.
${{M}_{O}}=\dfrac{\text{V}}{\text{U}}=\text{-}\dfrac{\text{L}}{{{\text{f}}_{\text{O}}}}\text{where L is the tube length and }{{\text{f}}_{\text{O}}}\text{ is the focal length of the objective}\text{.}$
An eyepiece acts as an simple microscope Hence magnification produced by the eyepiece is given by,
${{\text{M}}_{\text{E}}}\text{=}\dfrac{\text{D}}{{{\text{f}}_{\text{E}}}}\text{+1}$ . Substituting the magnifications of both the objective and the eyepiece in equation 1 we get,
$\begin{align}
  & m={{M}_{O}}{{M}_{E}} \\
 & m=\text{-}\dfrac{\text{L}}{{{\text{f}}_{\text{O}}}}\left( \dfrac{\text{D}}{{{\text{f}}_{\text{E}}}}\text{+1} \right) \\
\end{align}$
If we see the above equation the magnification of the compound microscope can be increased if we decrease the focal length of both the objective as well as the eye piece as they vary inversely.

Note: In actual practice each of the objectives and the eyepiece consists of a combination of lenses. To eliminate chromatic aberration, an objective consists of two lenses in contact. To reduce spherical aberration and chromatic aberration an eye piece consists of two lenses separated by a certain distance.