Question

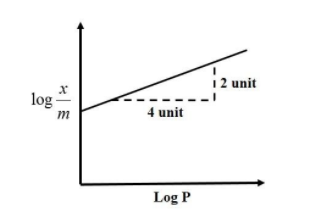
Adsorption of gas follows Freundlich adsorption isotherm. In the given plot, x is the mass of the gas adsorbed on the mass m of the adsorbent at pressure p. $\dfrac{{\text{x}}}{{\text{m}}}$ is proportional to:

(A) ${{\text{P}}^{\dfrac{{\text{1}}}{{\text{4}}}}}$
(B) ${{\text{P}}^{\text{2}}}$
(C) ${\text{P}}$
(D)${{\text{P}}^{\dfrac{{\text{1}}}{{\text{2}}}}}$

Answer 1

Hint: Knowledge on Freundlich adsorption isotherm is important to solve this question. The law states that the change in the amount of gas adsorbed by unit mass of a solid adsorbent is directly proportional to the change in the pressure, at a given temperature.
Formula used:
 $\dfrac{{\text{x}}}{{\text{m}}}{\text{ = K}}{{\text{P}}^{\dfrac{{\text{1}}}{{\text{n}}}}}$
Where, x is the mass of the gas adsorbed on the mass m of the adsorbent at pressure P, K is a constant.

Complete step by step answer:
The Freundlich equation is expressed as:
$\dfrac{{\text{x}}}{{\text{m}}}{\text{ = K}}{{\text{P}}^{\dfrac{{\text{1}}}{{\text{n}}}}}$
Taking log base 10 both sides:
$ \Rightarrow \log \dfrac{{\text{x}}}{{\text{m}}} = \log E + \dfrac{1}{{\text{n}}}\log {\text{P}}$ Where (n>1)........... (1)
                                                                    ........... (2)
From the equation of a straight line we know that:
${\text{y}} = {\text{mx}} + {\text{c}}$,
Where the intercept of the equation, c = 0, ${\text{y = mx}}$
Therefore, the slope of the equation, ${\text{m = }}\dfrac{{\text{y}}}{{\text{x}}}$
Substituting the values, we get:
${\text{m}} = \dfrac{2}{4} = \dfrac{1}{2}$
As per equation (1), the slope of the equation is $\dfrac{1}{2}$=$\dfrac{1}{n}$
So, $\dfrac{{\text{x}}}{{\text{m}}} = {\text{K}}{{\text{P}}^{\dfrac{1}{2}}}$

Hence, option (D) is the correct answer.

Note:
The Freundlich adsorption isotherm is not valid at high pressures. This is because, experimentally, it was seen that the extent of gas adsorption varies directly with the pressure raised to the power $\dfrac{{\text{1}}}{{\text{n}}}$ till the saturation pressure is reached.
The quantity \[\dfrac{{\text{x}}}{{\text{m}}}\] is called the extent of absorption of a gas.
The extent of pressure increases with the pressure and becomes maximum at a pressure known as the “Equilibrium pressure” (P).
At the equilibrium pressure the amount of the gas adsorbed becomes equal to the amount of the gas desorbed, as adsorption and desorption take place simultaneously at this pressure.
Some observations include:
At low pressures: $\dfrac{{\text{x}}}{{\text{m}}}{\text{ = KP}}$
At high pressures: $\dfrac{{\text{x}}}{{\text{m}}}{\text{ = K}}{{\text{P}}^{\text{0}}}$
When the value of the pressure lies from 0 to 1, $\dfrac{{\text{x}}}{{\text{m}}} = {\text{K}}{{\text{P}}^{\dfrac{1}{{\text{n}}}}}$